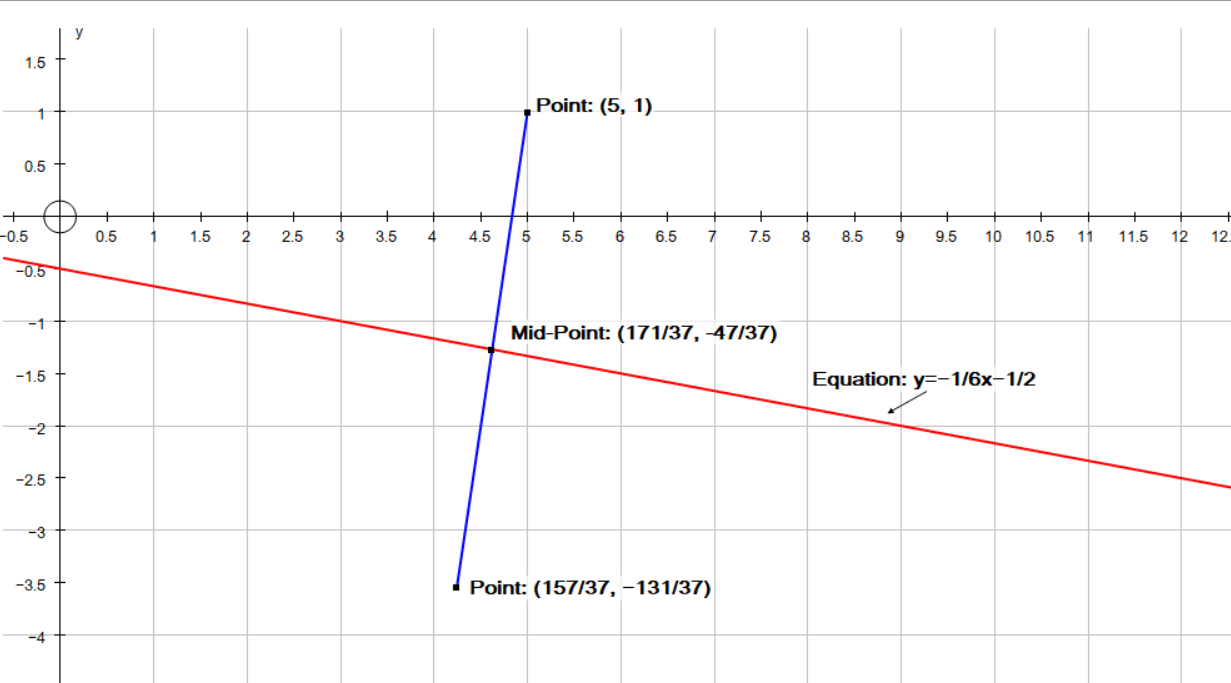
A line segment is bisected by a line with the equation $- 6 y - x = 3$ $-6 y - x = 3$ . If one end of the line segment is at $(5, 1)$ $( 5 , 1 )$ , where is the other end?

Question

A line segment is bisected by a line with the equation $- 6 y - x = 3$ $-6 y - x = 3$ . If one end of the line segment is at $(5, 1)$ $( 5 , 1 )$ , where is the other end?

2 Answers

Impact of this question

2578 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-23T12:08:23

Coordinates of the other end are $(\frac{167}{37}), - (\frac{84}{37})$ $(167/37), -(84/37)$

Explanation:

Assumption : The line bisecting the segment is its perpendicular bisector.

Eqn of line $x + 6 y = - 3$ $x + 6y = -3$ Eqn (1)
$6 y = - x - 3$ $6y = -x -3$
$y = - (\frac{x}{6}) - (\frac{1}{2})$ $y = -(x/6) - (1/2)$
Slope of the line is -(1/6)#

Slope of altitude the line segment is 6
Eqn of line segment is
$y - 1 = 6 (x - 5)$ $y -1 = 6 (x-5)$
$y - 6 x = 1 - 30 = - 29$ $y - 6x = 1-30 = -29$ Eqn (2)
Solving Eqns (1) & (2) we get the intersection of the lines or the midpoint of the line segment.
Coordinates of mid point are $(\frac{171}{37}), - (\frac{47}{37})$ $(171/37), -(47/37)$

$\frac{171}{37} = \frac{5 + x_{2}}{2}, - (\frac{47}{37}) = \frac{1 + y_{2}}{2}$ $171/37 = (5+x_2)/2, -(47/37) = (1+y_2)/2$ where $x_{2}, y_{2}$ $x_2, y_2$ are the coordinates of the other end point.

$x_{2} = (\frac{342}{37}) - 5 = \frac{167}{37}$ $x_2 = (342/37) -5 = 167/37$
$y_{2} = - (\frac{47}{37}) - 1 = - (\frac{84}{37})$ $y_2 = -(47/37)-1 = -(84/37)$

Answer 2 · 2017-11-23T13:33:57

$(\frac{157}{37}, - \frac{131}{37})$ $(157/37 , -131/37 )$

Explanation:

First we need to find the equation of the line that is perpendicular to the line $- 6 y - x = 3$ $-6y-x=3$ and passes through the point $(5, 1)$ $( 5 , 1 )$ . Since these lines are perpendicular we can find the gradient of the required line by using the fact that, if $m_{1}$ $m_1$ is the gradient of the known equation, then $m_{1} \cdot m_{2} = - 1$ $m_1*m_2=-1$

$:.$

$-1/6*m_2=-1=>m_2=6$

So second equation is:

$y-1=6(x-5)=>y=6x-29$

The point of intersection of these lines is the coordinates of the midpoint of the line segment.

Solving simultaneously:

$-1/6x-1/2=6x-29=>x=171/37$

$y=6(171/37)-29=-47/37$

We know for a line segment with coordinates $( x_1 , y_2)$ and $( 5 , 1 )$ , that the coordinates of the midpoint are $((5+x_1)/2 , (1+y_1)/2)$ .

Midpoint coordinates:

$(171/37 , -47/37 )$

$:.$

$(5+x_1)/2=171/37=>x_1 =157/37$

$(1+y_1)/2=-47/37=>y_1=-131/37$

Coordinates of end point of line segment:

$(157/37 , -131/37 )$

Plot:

enter image source here

Science

Math

Humanities

... and beyond

A line segment is bisected by a line with the equation $- 6 y - x = 3$ $-6 y - x = 3$ . If one end of the line segment is at $(5, 1)$ $( 5 , 1 )$ , where is the other end?

2 Answers

Explanation:

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

A line segment is bisected by a line with the equation -6 y - x = 3 −6y−x=3 -6 y - x = 3 . If one end of the line segment is at ( 5 , 1 )(5,1)( 5 , 1 ), where is the other end?

2 Answers

Explanation:

Explanation:

Related questions

Impact of this question

A line segment is bisected by a line with the equation $- 6 y - x = 3$ $-6 y - x = 3$ . If one end of the line segment is at $(5, 1)$ $( 5 , 1 )$ , where is the other end?