Question

A line segment is bisected by a line with the equation `-7 y + 3 x = 1`. If one end of the line segment is at `( 2 , 4 )`, where is the other end?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
Given :

(a) A line segment is bisected by a line.

(b) Equation of the line : `3x-7y=1`

Find :

If one end of the line segment is at `(2,4)`, find the other.

`color(green)("Step 1 :"`

Plot the point `A(2,4)` on a coordinate plane.

Graph the line `3x-7y=1` on the coordinate plane.

Construct a perpendicular line through the point `A(2,4)` to the line with the equation `3x-7y=1`.

This is the shortest distance between the line and the point `A(2,4).`

`color(green)("Step 2 :"`

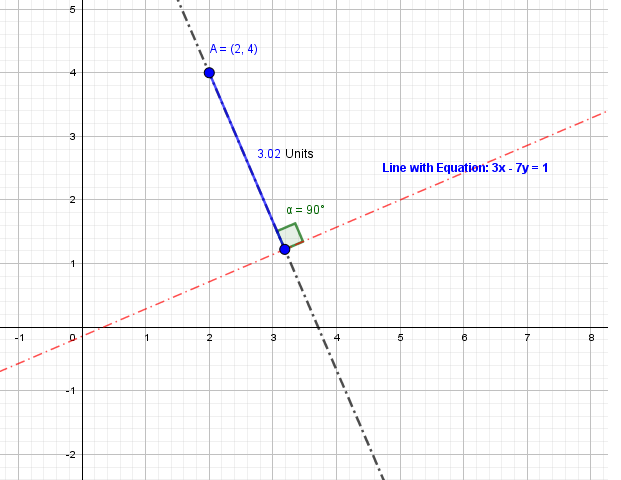
Mark the point of intersection of the perpendicular line and the line with the equation `3x-7y=1`.

This is the Mid-Point(O) of the required line segment we must find, in order to locate the coordinates of the other end of the line segment.

Measure the magnitude of `bar(AO)`.

`bar(AO)=3.02` units.

Using the Mid-Point (O) as the center, construct a circle with radius being the magnitude of the part of the line segment `AO`.

Radius `=3.02` units.

`color(green)("Step 3 :"`

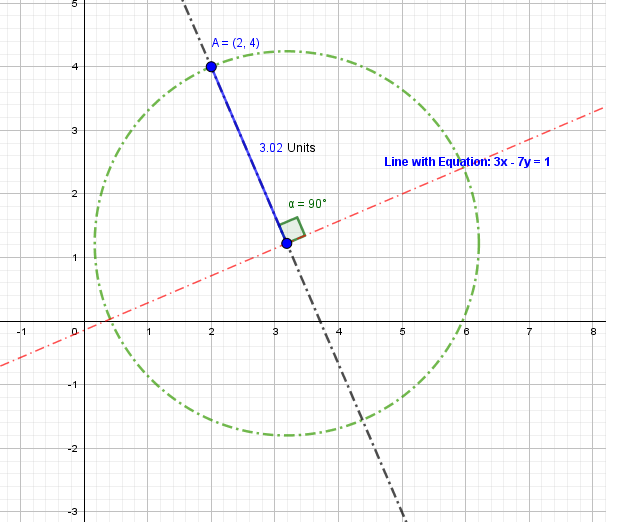
Extrend the line segment `AO` with a line.

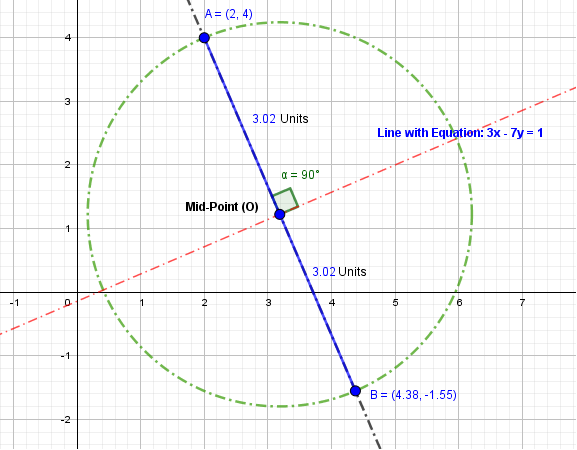
Mark the intersection of the circle and this part of the extended line.

This is our Point `B`.

Join `OB` and measure the magnitude of `bar(OB)`

`bar(OB)=3.02` units.

Find the coordinates of the point `B`.

`B=(4.38, -1.55)`. This is our required answer.

Hope you find this solution process useful to your requirement.