Question

A line segment is bisected by a line with the equation `-7 y + x = 3`. If one end of the line segment is at `(1 ,6 )`, where is the other end?

Answer 1

The other end of the bisected line could be any point on
`color(white)("XXX")-7y+x=47`

Explanation:

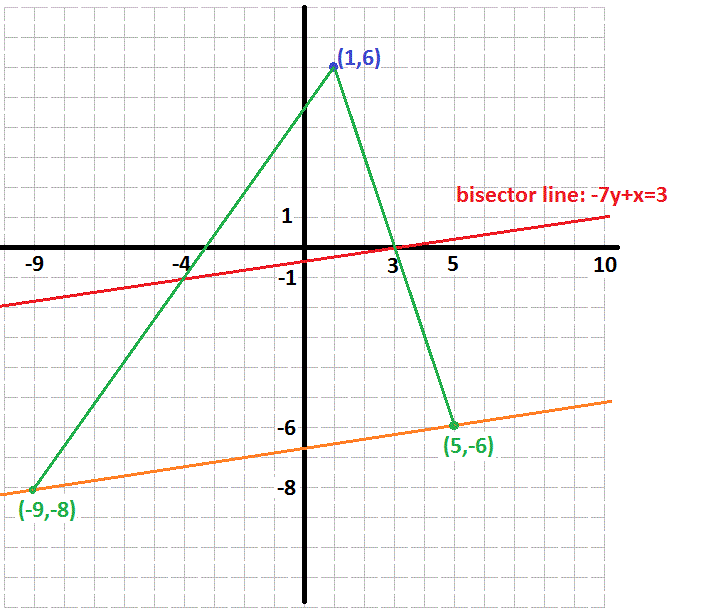
If `color(red)(-7y+x=3)` bisects a line segment between `color(blue)(""(1,6))` and some other point `color(green)(""(x',y'))`
with an intersection point of `color(red)(-7y+x=3)` and this line segment at `color(red)(""(barx,bary))`

Then
`color(white)("XXX")(6-color(red)(bary))=(color(red)(bary)-color(green)(y'))`
`color(white)("XXXXXX")rarr color(green)(y')=2color(red)(bary)-6`
and
`color(white)("XXX")(1-color(red)(barx))=(color(red)(barx)-color(green)(x'))`
`color(white)("XXXXXX")rarr color(green)(x')=2color(red)(barx)-1`

Specifically, we could solve `color(red)(-7y+x=3)` for a couple arbitrary solution points:
`color(white)("XXX")color(red)((barx_1,bary_1)=(-4,-1))`
and
`color(white)("XXX")color(red)((barx_2,bary_2)=(3,0))`

and obtain end-of-line-segment values:
`color(white)("XXX")color(green)((x'_1,y'_1)=(-9,-8))`
and
`color(white)("XXX")color(green)((x'_2,y'_2)=(5,-6)`

Using the slopes
`color(white)("XXX")(y-color(green)(y'_1))/(x-color(green)(x'_1))=(color(green)(y'_1-y'_2))/(color(green)(x'_1-x'_2))`

`color(white)("XXX")(y-color(green)(""(-8)))/(x-color(green)(""(-9)))=(color(green)(""(-8))-color(green)(""(-6)))/(color(green)(""(-9))-color(green)(""(-5)))`

`color(white)("XXX")(y+8)/(x+9)=1/7`

`color(white)("XXX")7y+56=x+9`

`color(white)("XXX")7y-x=-47`

or (paralleling the given form):
`color(white)("XXX")-7y+x=47`