Question

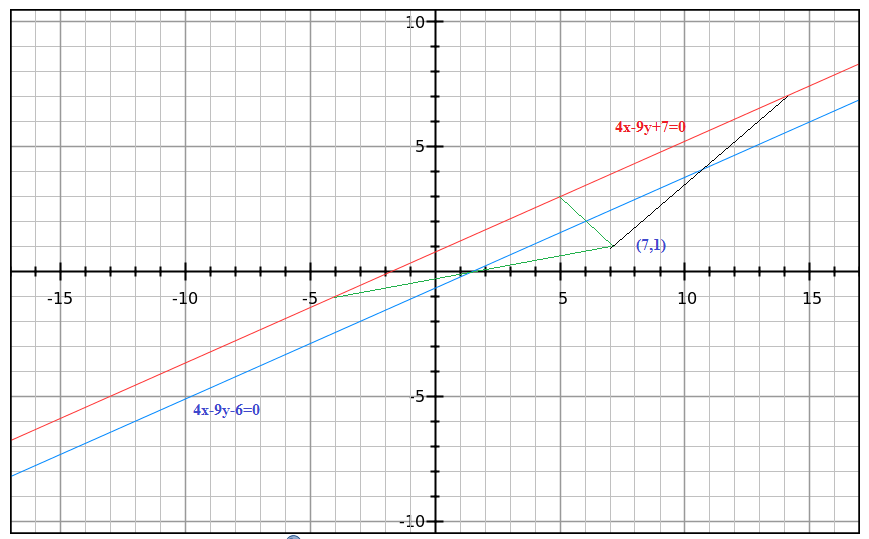
A line segment is bisected by a line with the equation `- 9 y + 4 x = 6`. If one end of the line segment is at `( 7 , 1 )`, where is the other end?

Answer 1

The coordinate of any point on the straight line represented by equation `4x-9y+7=0` ,will be the coordinate of other end point.

Explanation:

The coordinate of one end of the given line segment is (7,1).
Let the coordinate of other end be (h,k).

Hence the coordinate of its middle point is `((h+7)/2,(k+1)/2)`

The given line having equation `4x-9y=6........(1)` bisects the line segment.

So the mid point of the line segment is lying on the given straight line.
Hence its coordinate will satisfy the given equation.

So inserting `(x=(h+7)/2 and y=(k+1)/2)` in the given equation we have

`4xx(h+7)/2-9xx(k+1)/2=6`

`=>4h+28-9k-9=12`

`=>4h-9k+7=0`

Inserting x for h and y for k we get an equation of the straight line

as `4x-9y+7=0......(2)` which is a straight line parallel to the straight line represented by equation (1)

Hence the coordinate of any point on the straight line represented by equation `4x-9y+7=0......(2)` will be the coordinate of other end point.