Question

A line segment is bisected by a line with the equation `9 y + x = 5`. If one end of the line segment is at `( 7 , 4 )`, where is the other end?

Answer 1

The other end is: `( 249/41,-178/41)`
Here is a graph:

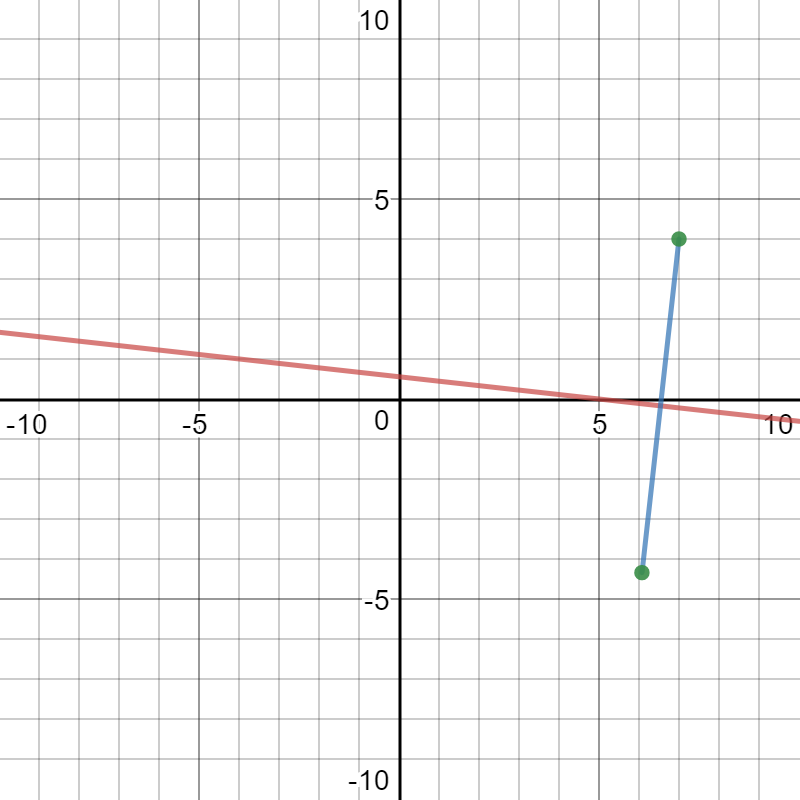
Explanation:

Given: `x+9y=5" [1]"`

The family of perpendicular lines is:

`9x-y=k`

Use the point `(7,4)` to find the value of x:

`9(7)-4=k`

`k = 59`

The equation of the bisected line is:

`9x-y=59" [2]"`

Multiply equation [2] by 9 and add to equation [1]:

`82x= 536`

`x_"midpoint" = 268/41`

Use the midpoint equation to find `x_"end"`

`x_"midpoint" = (x_"start"+x_"end")/2`

`268/41 = (7+x_"end")/2`

`x_"end" = 536/41-7`

`x_"end" = 249/41`

Find `y_"end"` by substituting `x_"end"` into equation [2]:

`9(249/41)-y_"end"=59`

`y_"end" = 9(249/41)-59`

`y_"end" = -178/41`