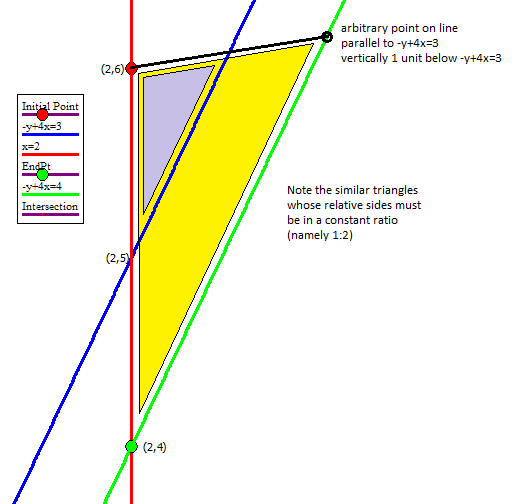
Consider the vertical line #color(magenta)(x=2)#
Clearly #color(magenta)x=2# goes through the point #color(red)(""(2,6))#
and it intersects #color(blue)(-y+4x=3)# at #color(blue)(""(2,5))#
#color(red)(""(2,6))# is vertically #color(brown)(1)# unit above #color(blue)(""(2,5))#, the intersection point with #color(blue)(-y+4x=3)#
#color(green)(""(2,4))# is vertically #color(brown)1# unit below #color(blue)(""(2,5))#, the intersection point with #color(blue)(-y+4x=3)#
Therefore #color(blue)(-y+4x=3)# bisects the line segment between #color(green)(""(2,4))# and #color(red)(""(2,6))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Furthermore (as seen in the image below and considering similar triangles)
any point on a line parallel to #color(blue)(-y+4x=3)# through #color(green)(""(2,4))# will provide, together with #color(red)(""(2,6))# a line segment bisected by #color(blue)(-y+4x=3)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)(-y+4x=3)# can be written in slope-intercept form as
#color(white)("XXX")color(blue)(y=4x-3)# with a y-intercept at #color(blue)(""(-3))#
If the line through #color(green)(""(2,4))# parallel to #color(blue)(-y+4x=3)# is #color(brown)(1)# unit vertically below #color(blue)(-y+4x=3)#
it will have a y-intercept at #color(green)(""(-4))#
and therefore a slope-intercept form of
#color(white)("XXX")color(green)(y=4x-4)#

