Given:#" "3y+7x=4#
Write as #color(blue)(y=-7/3x+4/3" "larr" first line")....(1)#
Thus the gradient of the line normal to this (perpendicular) is:
#(-1)xx1/m" "->" "(-1)xx(-3/7)=+3/7# giving:
#" "color(blue)(y=3/7x+c" "larr" second line")......(2)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Determine the value of "c)#
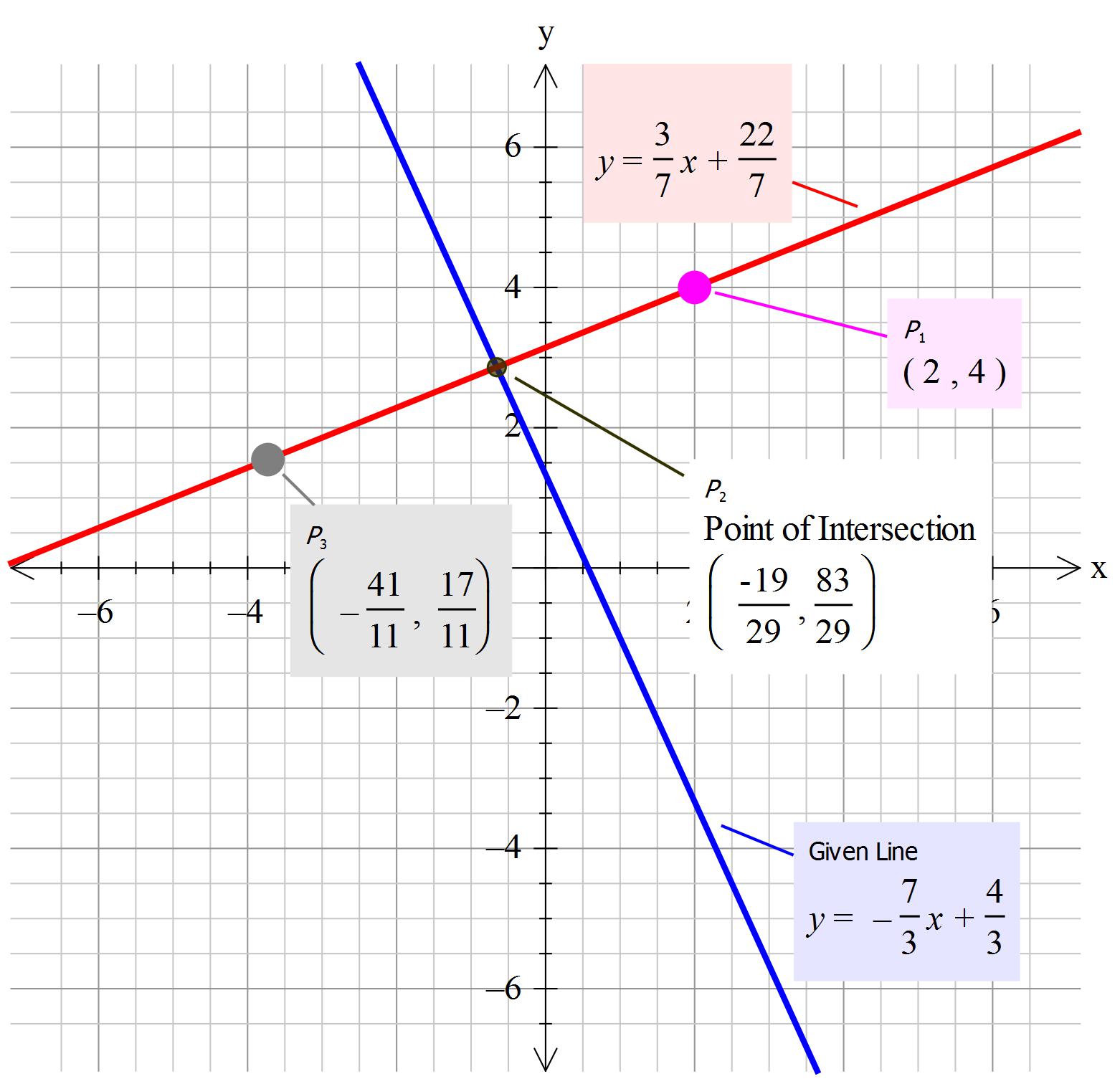
The second line passes through the point #P_1->(x,y)->(2,4)#
so by substitution:
#color(red)(y=3/7x+c)color(green)(" "->" "4=3/7(2)+c)#
#c" "=" "4-6/7" "=" " 3 1/7 -> 22/7# giving:
#" "cancel(color(blue)(y=3/7x+19/7" "larr" second line")...(3))#
#" "color(blue)(y=3/7x+color(red)(22/7)" "larr" second line corrected")...(3)" "#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Determine point of intersection " P_2)# (mid point)
Relating equation (3) to equation (1) through #y#
#" "3/7x+22/7" "=" "y" "=" "-7/3x+4/3#
#" "=>3/7x+7/3x" "=" "4/3-22/7#
#" "(9+49)/21x" "=" "(28-66)/7#
#" "58x" "=" "-38#
#" "x=-38/58" "->" "-19/29#
#" "P_2->(x,y)=(-19/29 , y )#
substitute into equation (3) to find #P_2(y)#
#" "y=3/7x+22/7" "->" " y=3/7(-19/29)+ 22/7#
#" "y=2 25/29 -> 81/29#
#color(blue)(" "P_2->(x,y)=(-19/29 , 81/29 ))#
,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Determine point "P_3)#
#P_1(x)" to "P_2(x)" " =" " P_2(x)-P_1(x)#
#" "=" "2-(-19/22) = 2 19/22#
,................................................................................................
#" "P_3(x)" "=" "P_1(x)-2(2 19/22)#
#" "P_3(x)" "=" "2-2(2 19/22)" "=" "-3 8/11#
'.............................................................................................
Substitute for #x# in equation (3) to find #P_3(y)#
#P_3(y)=3/7x+22/7" "->" "3/7(-3 8/11)+22/7#
#P_3(y)=1 6/11#
'.........................................................................................
#P_3(x,y)=(-3 8/11,1 6/11)#


