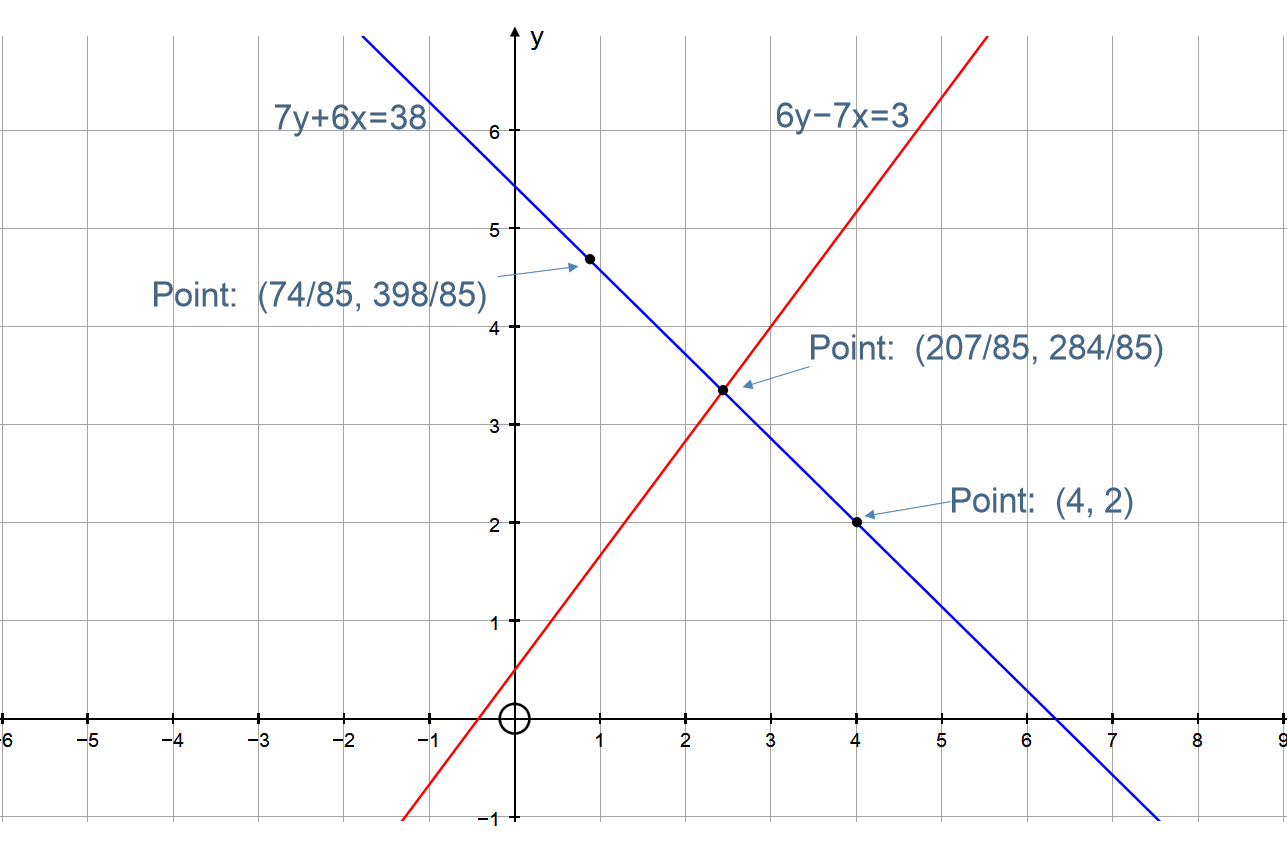
A line segment is bisected by line with the equation # 6 y - 7 x = 3 #. If one end of the line segment is at #(4 ,2 )#, where is the other end?
1 Answer
Explanation:
First we note that if two lines are perpendicular then the product of their gradients is
We need to find the equation of a line that contains the point
Rearranging
If the gradient for our given line be
Using point slope form of a line:
Finding the point of intersection.
Solve
Substituting in
The coordinates for the midpoint of a line is given by:
Therefore:
Hence:
Coordinates of the other end are:
PLOT: