A line segment with endpoints at #(1, 5)# and #(1, -2)# is rotated clockwise by #pi/2#. What are the new endpoints of the line segment?
1 Answer
Feb 1, 2016
Explanation:
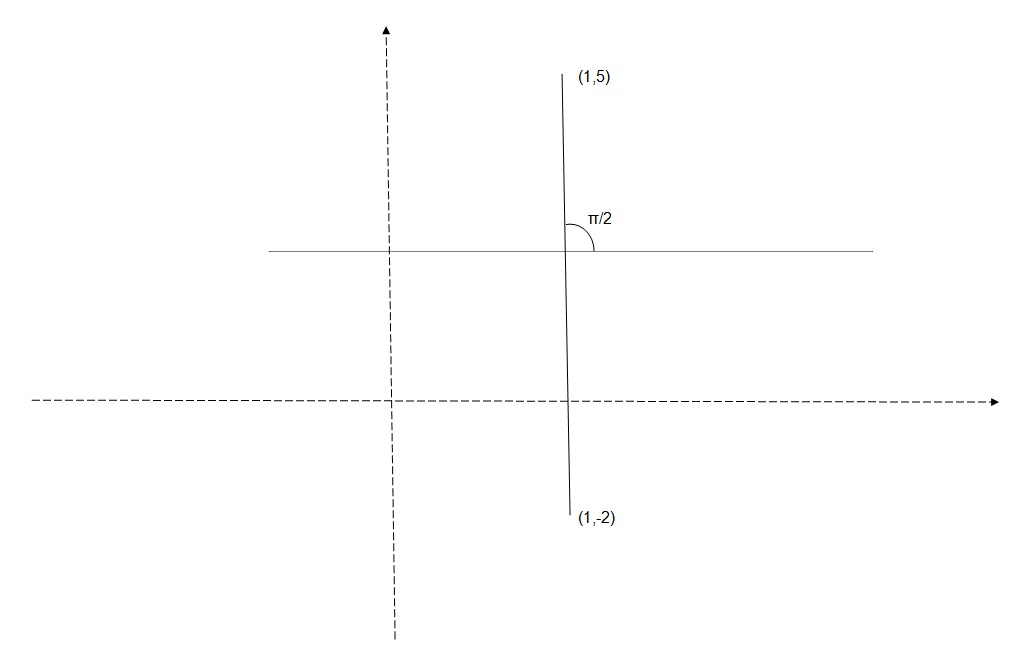
The length of the line is
Because the line is now horizontal the new end points are

