Question

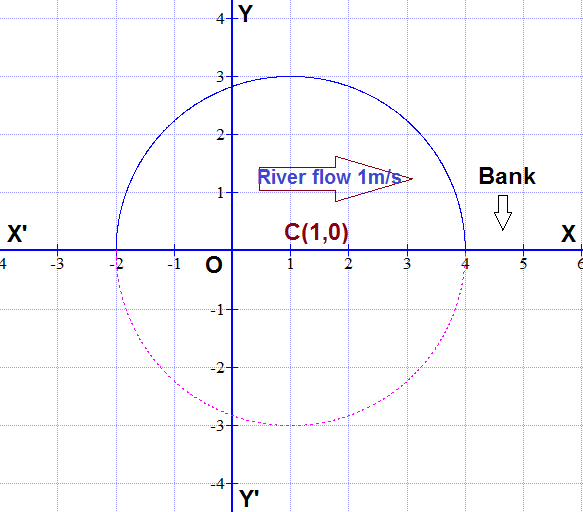
A man can swim in still water with a speed of 3 m/s. `x` and `y` axes are drawn along and normal to the bank of the river flowing to right with a speed of 1 m/s. The man starts swimming from origin `O` at `t=0` second. Assume size ............?

A man can swim in still water with a speed of 3 m/s. `x` and `y` axes are drawn along and normal to the bank of the river flowing to right with a speed of 1 m/s. The man starts swimming from origin `O` at `t=0` second. Assume size of man to be negligible. Find the equation of locus of all possible points where man can reach at `t=1 sec`?

Answer 1

Suppose the swimmer swims with velocity `3` m/s in the direction making an angle `theta` with the bank i.e positive direction of X-axis,OX

So the velocity components of the swimmer will be

`V_(OX)=3costheta`

and

`V_(OY)=3sintheta`

As the river is flowing along `OX`

Net velocity along `OX` will be `3costheta+1`

These two velocities are independent on each other as they are orthogonal. The swimmer starts at origin `O` If the displacement of the swimmer after 1 sec along X-axis and Y- axis be `x and y` respectively then

`x=3costheta +1......[1]`
and
`y=3sintheta.............[2]`

From [1] and [2] we get

`(x-1)^2+y^2=3^2cos^2theta+3^2sin^2theta=9`

So equation of locus of all possible points where man can reach at t=1sec will be

`color(magenta)((x-1)^2+y^2=3^2)`, the possible positions are on the blue semicircular line of radius 3m and center `C(1,0)` as shown in figure above.