Question

A neutron breaks into a proton and an electron. This decay of neutron is accompanied by the release of energy.Assuming that 50% of the energy is produced in the form of electromagnetic radiation, what will be the frequency of radiation produced.?

Answer 1

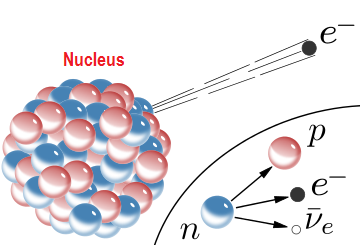
1st part
A free neutron decays forming particles such as proton `(p)` ,electron `(c^-)` and antineutrino `(barnu_e)` along with electromagnetic radiation in the form of `gamma`-ray

`n->p+e^(-)+ barnu_e+gamma`

Here the mass difference occurring for this transformation goes to the formation of electromagnetic radiation.

Initial mass.

the mass of neutron `m_n= 939.5656 MeV`

Final mass

the mass of proton `m_p= 938.2723 MeV`

the mass of electron `m_e=0.5100 MeV`

So mass difference (neglecting mass of antineutrino

`Deltam=m_n-m_p-m_e=0.7833MeV`

So total energy produced `DeltaE=0.7833MeV`

As per problem `50%` of total energy is produced in the form of electromagnetic radiation.

So radiated energy `DeltaE_"rad"=1/2DeltaE=0.3917MeV`

So frequency of radiation `nu=(DeltaE_"rad")/h`.

`=>nu=(0.3917xx10^6eV)/(4.1356xx10^-15eVs)=color(red)(9.4714xx10^19Hz)`.

where `h->"planck's constant"=4.1356xx10^-15eVs`

2nd part

Given 1st ionization energy of Al

`E_"ionisation"=577kJmol^(-1)`

`=577kJmol^(-1)xx1/(1.6022xx10^-22(kJ)/(eV))xx1/(6.022xx10^23mol^-1)`

`=5.98eV=5.98xx10^-6MeV`

So this energy is needed to remove first electron from the outermost shell of an atom of Al in its lowest energy state.

The energy of radiation `DeltaE_"rad"=0.3917MeV` being much higher than 1st ionization energy of Aluminum atom electron will be ejected absorbing the energy of photon of the given radiation,

The energy of the ejected electron

`E_"electron ejected"=DeltaE_"rad"-E_"ionisation"`