A plane, whose speed in still air is 360 km/h flies directly from London to Rome, at a distance of 1400 km. The bearing of Rome from London is 135 degree and there is wind of 120 km/h blowing from North? Find?(see below)
(a) the course set by the pilot and
(b) the time, in minutes, for the flight.
(a) the course set by the pilot and
(b) the time, in minutes, for the flight.
1 Answer
(A) An angle of 121.37 degrees.
(B) A time of 3.22 hours.
Explanation:
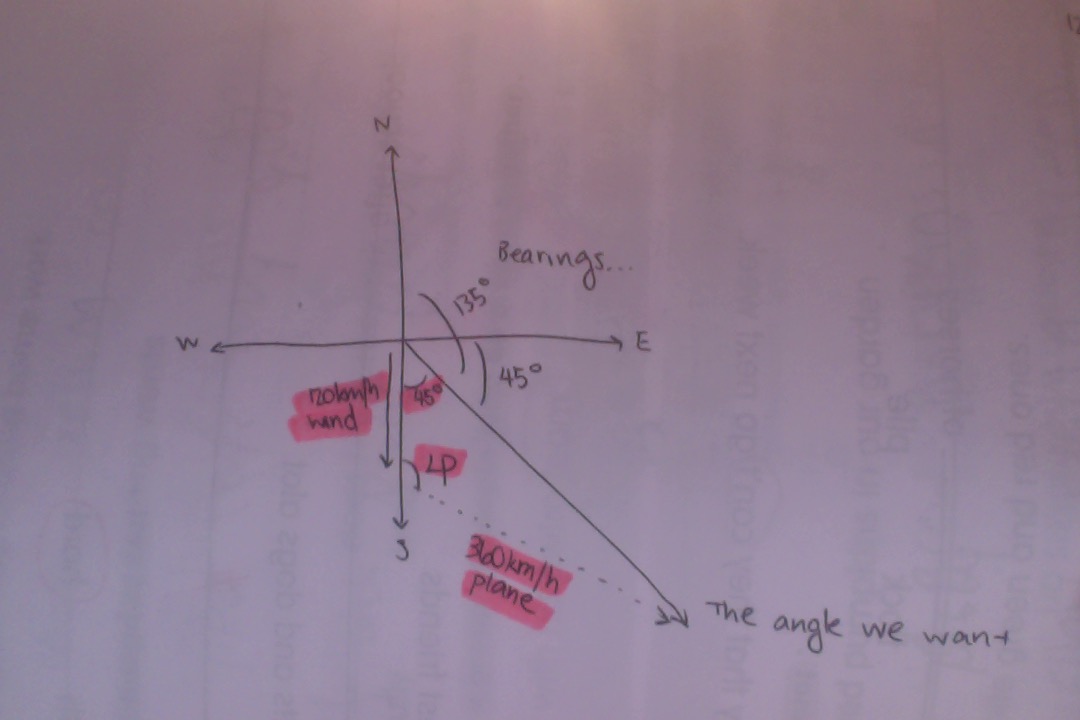
First, this is what bearings mean, I think. I also looked at a map of Europe, and this seems to be about right.

So 135 degrees actually directs SE at 45 degrees below the horizontal.
Now, think in vectors. We have two "movement" vectors, the wind, and the plane. If we add these vectors together, we want a vector that points to our "135" degrees. We know the magnitude of both vectors, but we don't know the direction of the planes vector. That is what we should find first. Lets set that angle as
In order to solve for
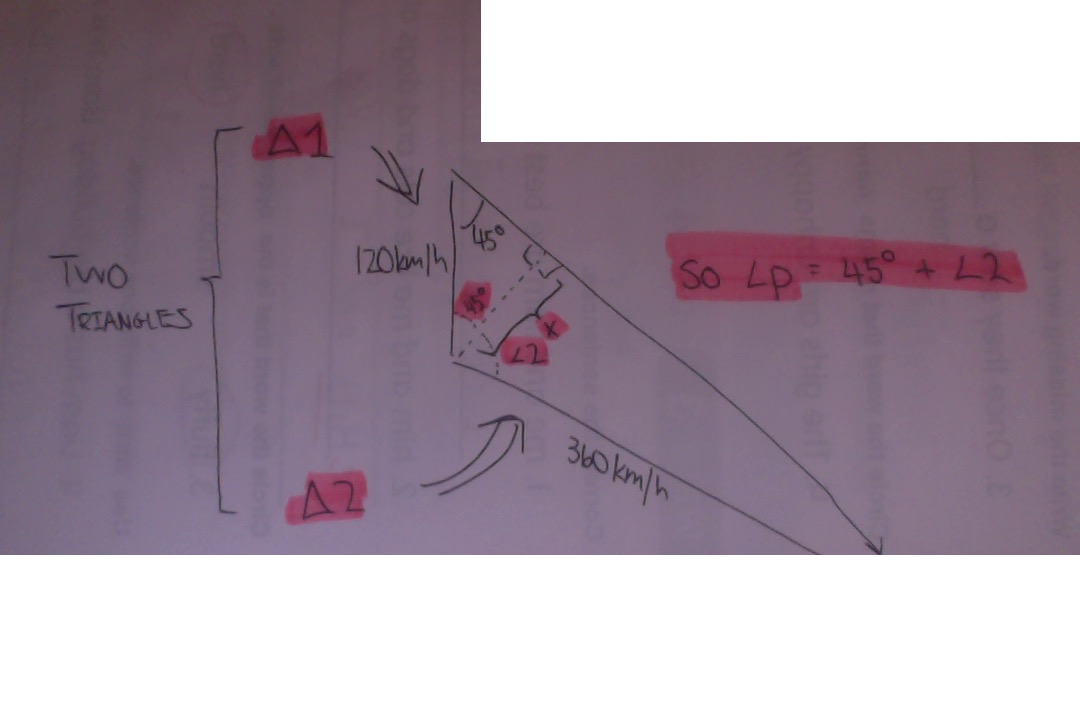
For triangle 1, we need to find the side length. This is a 45°-45°-90° triangle, so you can use trig or the pythagorean theorem to solve for the length. You should find that the length of one side is roughly 84.85 km/hour. This side length is also a side length to Triangle 2, so that will help us on our next calculation.
For Triangle 2, we now know the missing side length (84.85km/hour) so we can find
Now we know that
That is the answer to part A.
For part B, we need to find the speed that the plane reaches its destination, is the result of adding the two "movement" vectors, the wind velocity and the plane velocity.
The easiest way would be to use the law of cosines to find the hypotenuse of the triangle.
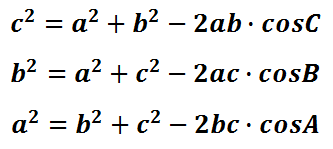
So the velocity is
So the velocity the plane reaches its destination is 434.7km/h
Finally, we use this velocity to find the total time traveled using the equation
Thus, if the distance is 1400km, then the time is

