A projectile is shot at a velocity of #37 m/s# and an angle of #pi/12 #. What is the projectile's maximum height?
2 Answers
The maximum height is
Explanation:
The maximum height is obtained from the formula
The vertical component of the velocity is
At the maximum height,
So,
The maximum height of the projectile is
Explanation:
To find the projectile's maximum altitude, or maximum height, we can make use of kinematic equations. Namely,
Because the projectile is launched at an angle, it is necessary to break up the given initial velocity into horizontal and vertical components. This can be done using basic trigonometry.
We take the initial velocity to be
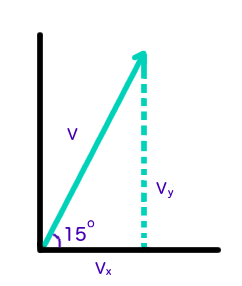
Note: Diagram not to scale.
For this problem, we require only the vertical velocity component.
As we know that
We will assume this to be the initial vertical velocity of the projectile, while the final vertical velocity of the projectile will be
Because this object is in free-fall, its vertical acceleration is equal to
Rearrange to solve for
The maximum altitude of the projectile is


