A projectile is shot at an angle of #(5pi)/12 # and a velocity of # 4 m/s#. How far away will the projectile land?
1 Answer
The projectile will land
Explanation:
As the projectile is launched at an angle, we will need to break the given velocity up into its
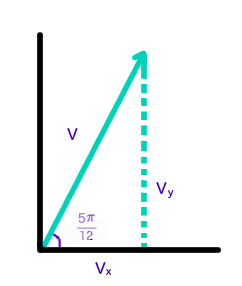
Using basic trigonometry, we can see that
We will calculate both of these components, then use the
Assuming the launch and landing points of the projectile are at the same altitude, the total flight time of the projectile is twice the flight time between the launch and the maximum altitude of the projectile. We can find
This kinematic will do the trick:
The total flight time is then
Now we can use this kinematic to find the range of the projectile:
Where
Hope that helps!

