Question

A projectile is shot at an angle of `pi/12` and a velocity of `88 m/s`. How far away will the projectile land?

Answer 1

For Physics or Mechanics you should learn the "suvat" equations for motion under constant acceleration:

`{: (v=u+at, " where ", s="displacement "(m)), (s=ut+1/2at^2, , u="initial speed "(ms^-1)), (s=1/2(u+v)t, , v="final speed "(ms^-1)), (v^2=u^2+2as, , a="acceleration "(ms^-2)), (s=vt-1/2at^2, , t="time "(s)) :}`

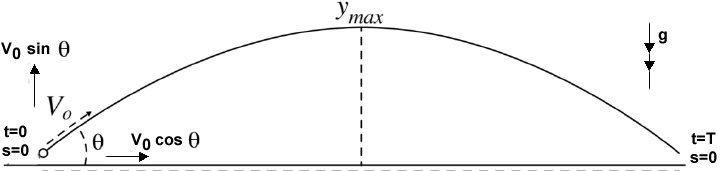
Vertical Motion
Motion under constant acceleration due to gravity, applied vertically upwards

Let the total time that the projectile takes to its return to the ground after launch be `T`, We would expect two solutions as obviously T=0 is one solution. The total displacement will be zero.

`{ (s=,0,m),(u=,88 sin(pi/12),ms^-1),(v=,"not required",ms^-1),(a=,-g,ms^-2),(t=,T,s) :}`

So we can calculate `T` using `s=ut+1/2at^2`

`:. 0 = 88sin(pi/12)T + 1/2(-g)T^2`
`:. 1/2gT^2-88sin(pi/12)T=0`
`:. T((gT)/2-88sin(pi/12)) =0`
`:. T =0, T = (176sin(pi/12))/g`

Horizontal Motion
Under constant speed (NB we can still use "suvat" equation with a=0). Thje projectile will be in in the air for the same time, `t =T`

So we can calculate the horizontal displacement `s` using `s=ut`

`s = 88cos(pi/12)T`
`:. s = (88cos(pi/12)(176sin(pi/12)))/g`
`:. s = (176*44*2cos(pi/12)sin(pi/12))/g`
`:. s = (7744sin((2pi)/12))/g`
`:. s = ((7744)(0.5))/g`
`:. s = 3872/g`

So using `g=9.8 ms^-2` we have.

`s=3872/9.8 = 395.102...= 395 m`