Question

A projectile is shot at an angle of `pi/6` and a velocity of `3 2 m/s`. How far away will the projectile land?

Answer 1

`x_m=90.40" "m`

Explanation:

`"please look over the animation carefully"`
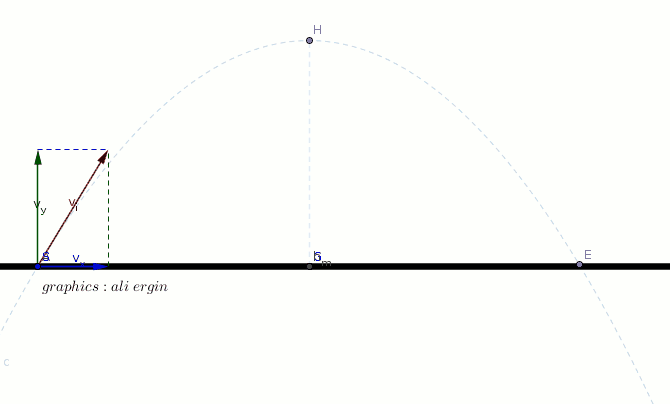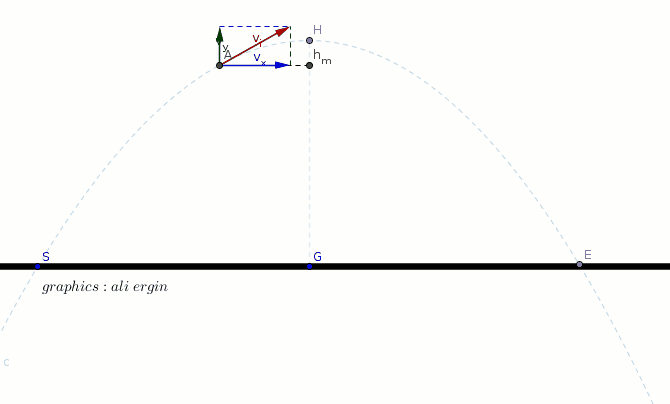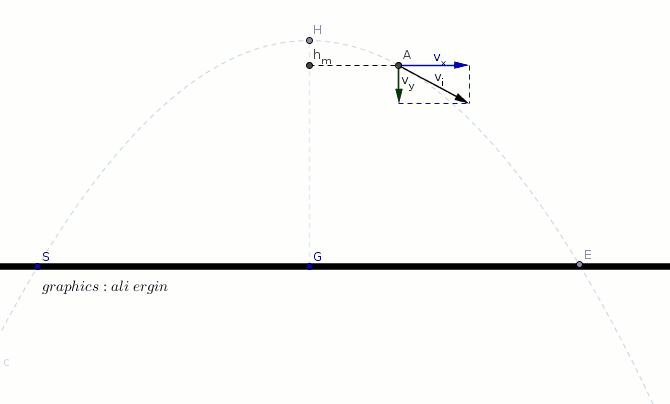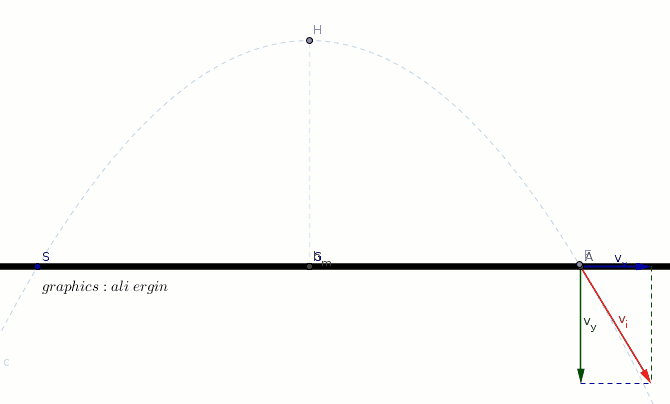
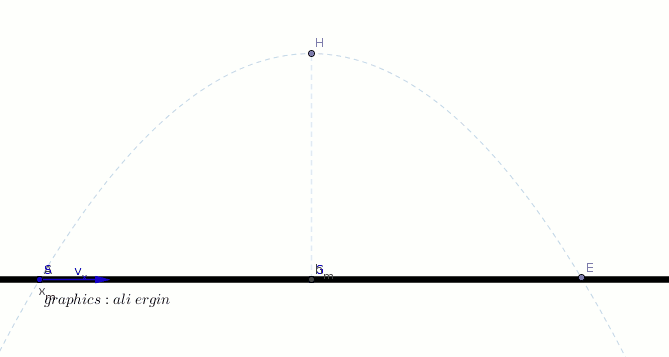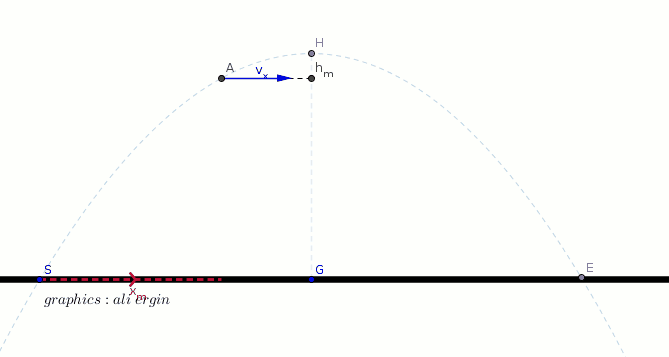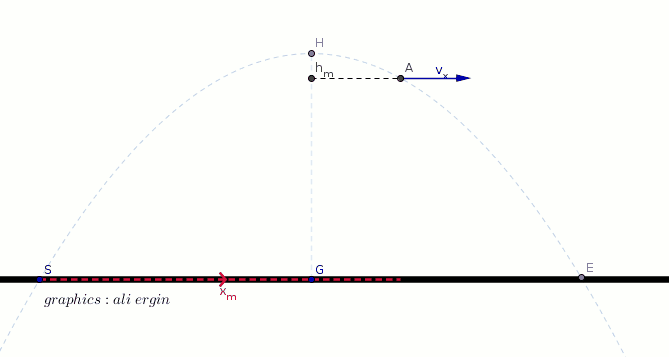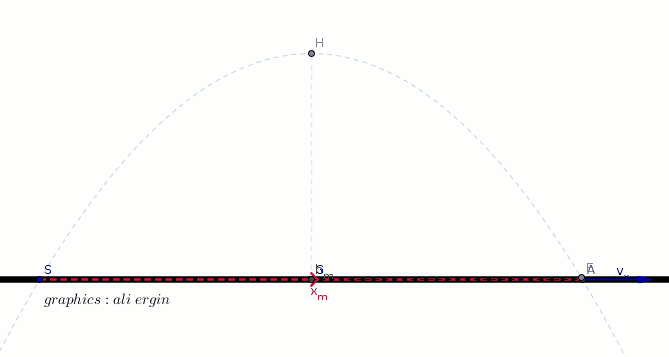
`"The initial velocity of object can be split into two components"`
`"as vertical and horizontal. "(v_x,v_y)`

`v_x=v_i*cos alpha`
`v_y=v_i*sin alpha-g*t`

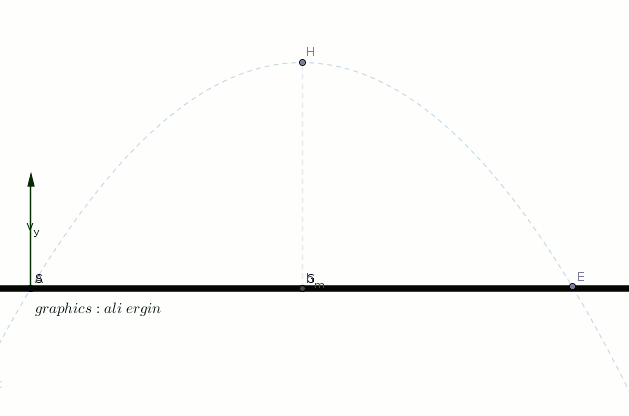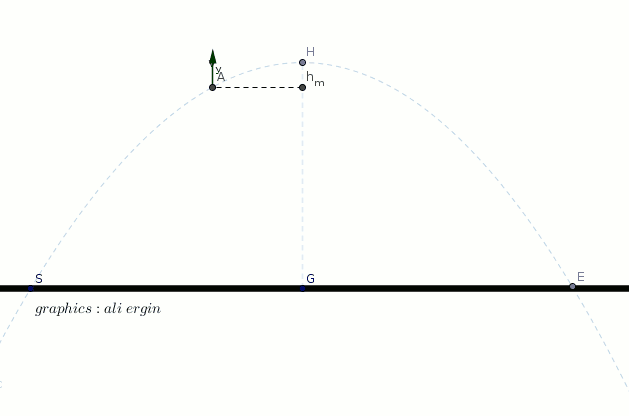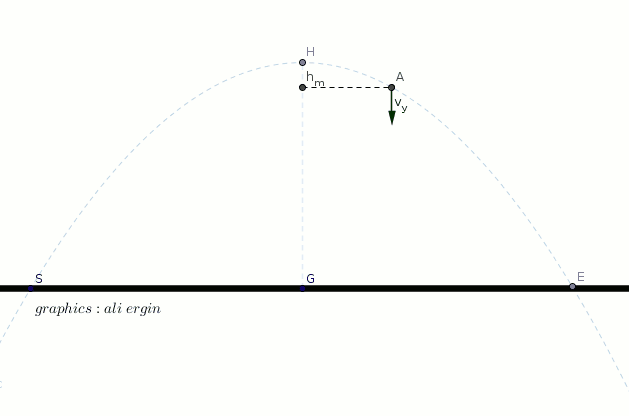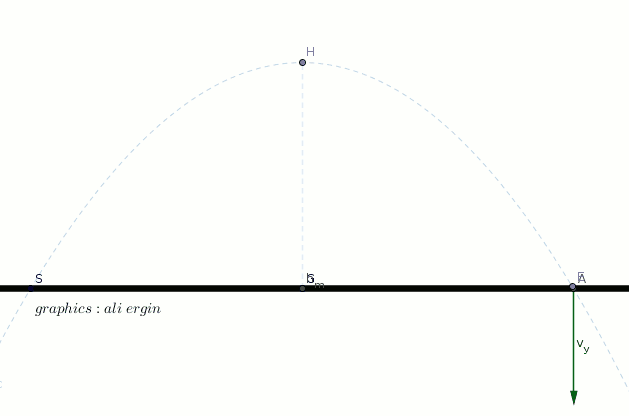
`"we can find the time elapsed using the component "v_y`

`"we can write "v_y=0 " for the maximum height."`

`v_y=v_i*sin alpha-g*t=0`

`v_i*sin alpha=g*t`

`t=(v_i*sin alpha)/g`

`t_f:"represents the flaying time"`

`t_f=2*t=(2*v_i*sin alpha)/g`

`x_m=v_x*v_f`

`x_m=(v_i*cos alpha*2*v_i*sin alpha)/g`

`x_m=(v_i^2*2*sin alpha*cos alpha)/g`

`2*sin alpha*cos alpha=sin 2 alpha`

`x_m=(v_i^2*sin 2alpha)/g`

`"where:"`
`v_i=32" "m/s`
`2*alpha=pi/6*2=pi/3`
`g=9.81" "m/s^2`

`x_m=(32^2*0.866)/(9.81)`

`x_m=90.40" "m`