A projectile is shot at an angle of #pi/8 # and a velocity of # 27 m/s#. How far away will the projectile land?
1 Answer
52.59m
Explanation:
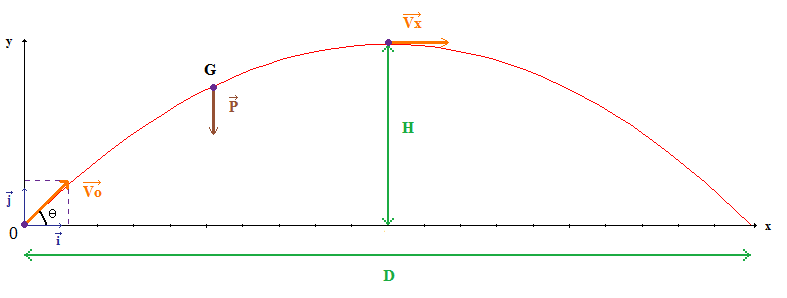
We have to calculate the initial speed in x and in y:
We have to know when the projectile will land.
We are going to calculate when the projectile is at its maximum height and multiply it by 2. Let's use the equation of the speed (velocity) for an object with acceleration:
The acceleration is
And to find the time it took the projectile to land we multiply this answer by 2:
To find the distance in x we have to use the equation of distance:
Theres no acceleration and
We could have used a formula to calculate it directly:
This method is explained in this answer:
https://socratic.org/questions/a-projectile-is-shot-at-an-angle-of-pi-8-and-a-velocity-of-65-m-s-how-far-away-w?source=search

