A projectile is shot from the ground at an angle of #pi/12 # and a speed of #8 /3 m/s#. Factoring in both horizontal and vertical movement, what will the projectile's distance from the starting point be when it reaches its maximum height?
1 Answer
At its maximum height, the projectile will have traveled a horizontal distance of
Explanation:
We want to calculate the range of the projectile at its maximum altitude.
Begin by breaking the initial velocity into components. Given that
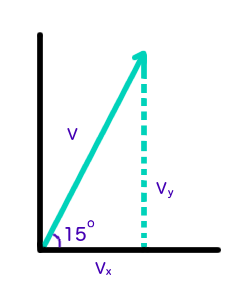
Where
#pi/12=15^o#
Using basic trigonometry, we can see that the perpendicular (vertical,
#sin(theta)=(opp.)/(hyp.)#
#=>sin(theta)=(v_y)/(v)#
#cos(theta)=(adj.)/(hyp.)#
#=>cos(theta)=(v_x)/v#
We can rearrange to solve for
#v_y=vsin(theta)#
#=>v_y=(8/3m/s)sin(pi/12)#
#=>v_y~~0.69m/s# -
#v_x=vcos(theta)#
#=>v_x=(8/3m/s)cos(pi/12)#
#=>v_x~~2.58m/s#
At the projectile's maximum altitude, it will have
We can then put this value for
Calculating
#v_f=v_i+a_yDeltat#
#Deltat=(v_f-v_i)/a_y#
#Deltat=(0-0.69m/s)/(-9.8m/s^2)=0.070s#
Now we calculate how far the projectile has traveled horizontally (i.e. the range) in this amount of time. Remember that there is no horizontal acceleration.
#Deltax=v_iDeltat+cancel(1/2aDeltat^2)#
#Deltax=(2.58m/s)(0.070s)~~0.18m#

