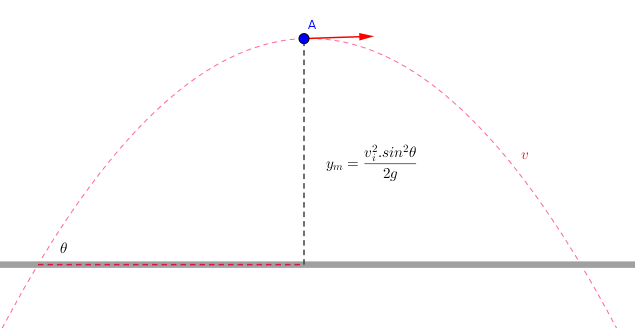
A projectile is shot from the ground at an angle of #pi/4 # and a speed of #8 m/s#. Factoring in both horizontal and vertical movement, what will the projectile's distance from the starting point be when it reaches its maximum height?
2 Answers
The distance is
Explanation:
Resolving in the vertical direction
initial velocity is
Acceleration is
At the maximum height,
We apply the equation of motion
to calculate the time to reach the greatest height
The greatest height is
Resolving in the horizontal direction
To find the horizontal distance, we apply the equation of motion
The distance from the starting point is
Please check the animations carefully. The answer is given at the end of the explanation.
Explanation:
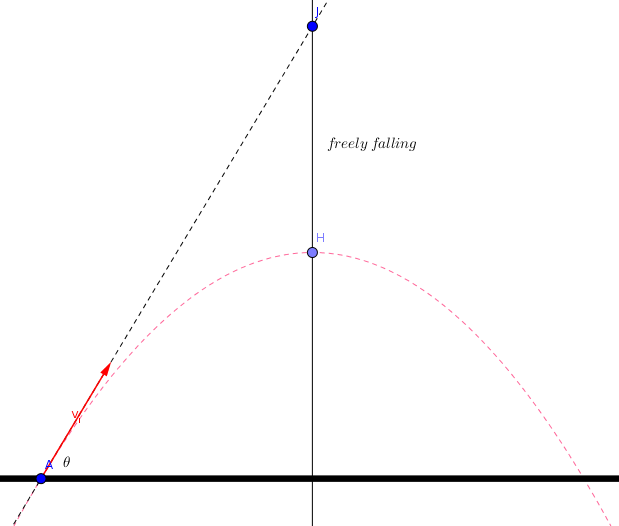
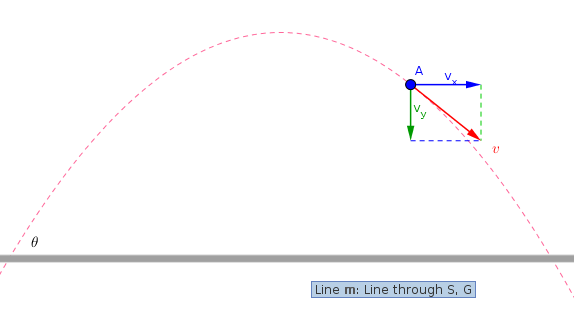
- The blue vector shows the horizontal component of the initial velocity.
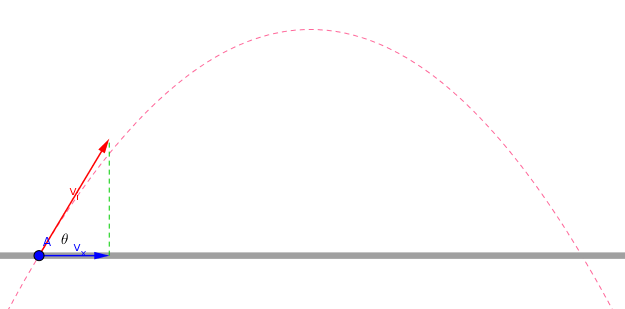
- The magnitude and direction of blue vector does not change.
- *The blue vector allows the object to move horizontally. *
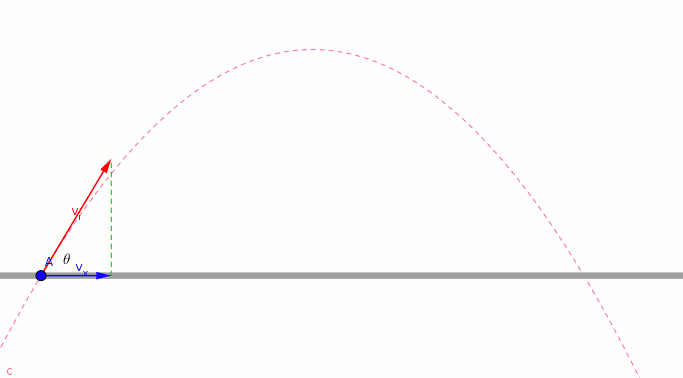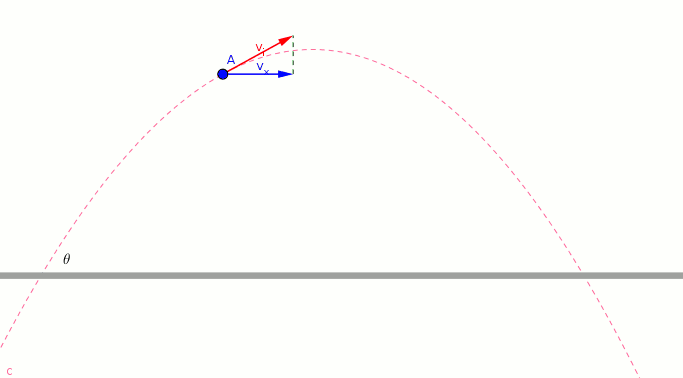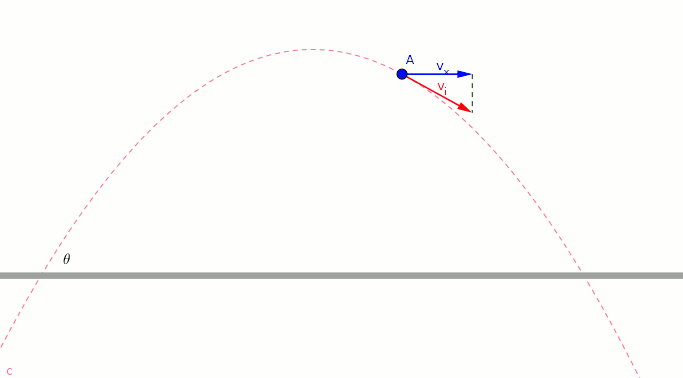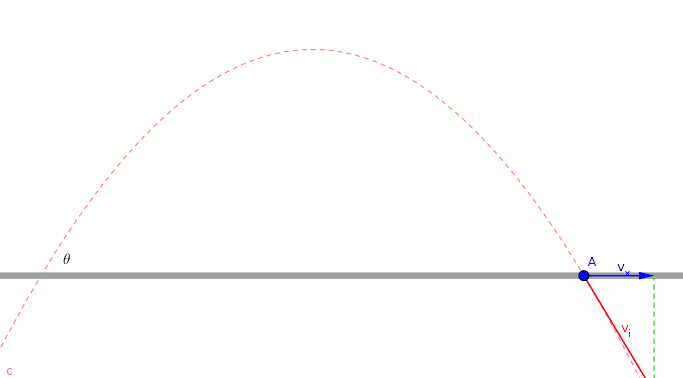
- The green vector shows the vertical component of the initial velocity.
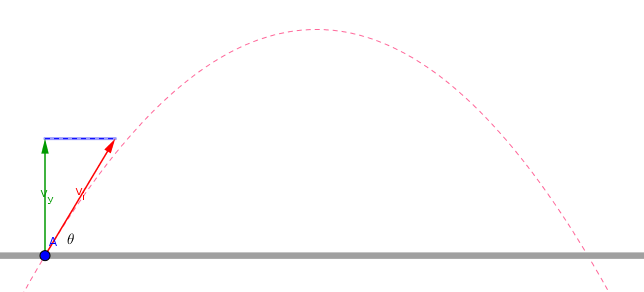
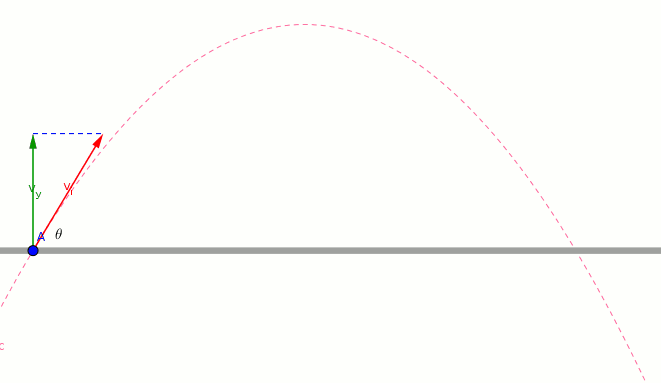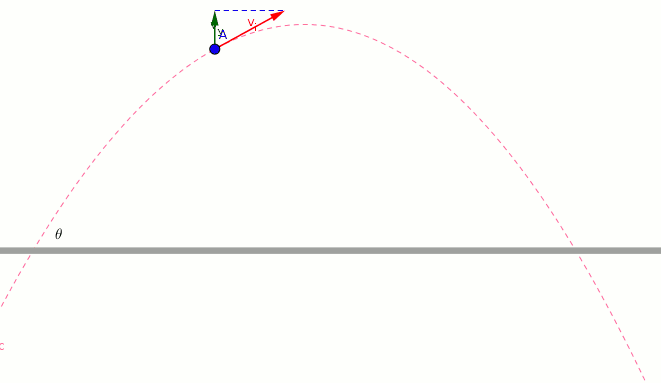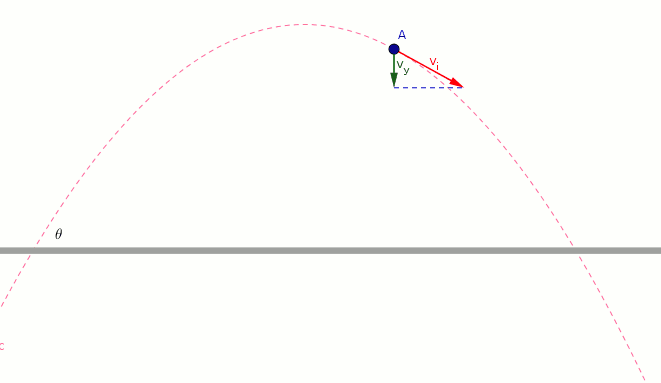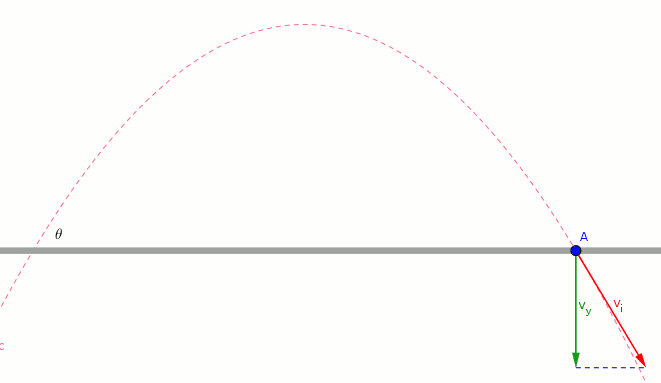
- The magnitude and direction of green vector change.
- *The blue vector allows the object to move vertically. *
- the magnitude of green vector at maximum height is zero.