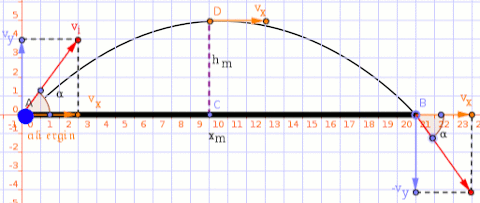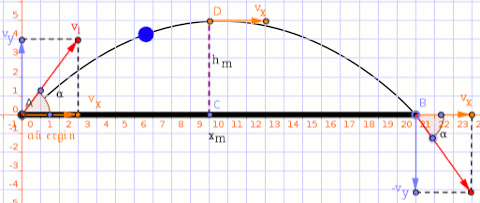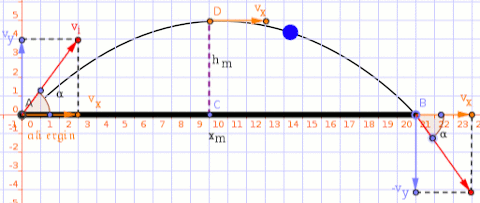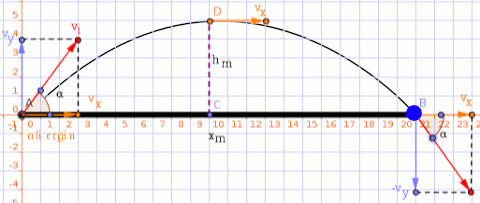
A projectile is shot from the ground at an angle of #pi/6 # and a speed of #15 m/s#. Factoring in both horizontal and vertical movement, what will the projectile's distance from the starting point be when it reaches its maximum height?
1 Answer
Mar 8, 2016
Explanation: