A projectile is shot from the ground at an angle of #pi/6 # and a speed of #5 m/s#. When the projectile is at its maximum height, what will its distance, factoring in height and horizontal distance, from the starting point be?
1 Answer
dx=0,22 m dy=0,9566
Explanation:
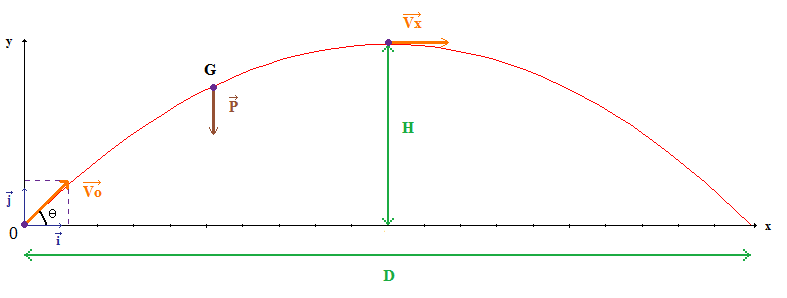
We have to calculate the initial speed in x and in y:
Let's calculate the distance in y (height):
We have to know when is the projectile at its maximum height. Let's use the equation of the speed for an object with acceleration:
The acceleration is
To find the distance in y we have to use the equation of distance:
To find the distance in x we have to use another time the equation of distance (this time there's no acceleration):

