A projectile is shot from the ground at an angle of #pi/8 # and a speed of #7 /12 m/s#. Factoring in both horizontal and vertical movement, what will the projectile's distance from the starting point be when it reaches its maximum height?
1 Answer
The projectile will be
Explanation:
We can find the projectile's horizontal displacement when it reaches its maximum altitude using kinematics . We will first make the assumption that air resistance and all other outside forces are negligible and consider only the effects of the force of gravity.
We are given the following information:
-
#->theta=pi/8# -
#->v_i=7/12"m"//"s"#
My approach would be to calculate the time elapsed between the object's launch and when it reaches its maximum altitude, and then use that value to calculate the horizontal distance it covers in the same amount of time. You can then calculate the vertical distance traveled and combine these components for an overall displacement (and not necessarily in that order).
-
At the top of the object's trajectory, its maximum altitude, the velocity of the object is instantaneously zero as it changes direction.
-
Additionally, because the object is a projectile assumed to be under the force of gravity alone, the object is in free-fall, and therefore has an acceleration equal to the negative of the gravitational acceleration (free-fall) constant,
#g# . This acceleration occurs only in the downward direction, and there is no horizontal acceleration.
We now have the following information:
-
#->theta=pi/8# -
#->v_i=7/12"m"//"s"# -
#->v_f=0# -
#->a_y=-9.8"m"//"s"^2# -
#->a_x=0#
We will use the following kinematic equation and solve for
#color(purple)((v_f)_y=(v_i)_y+a_yDeltat)#
Now, before we can use this equation, we will have to find
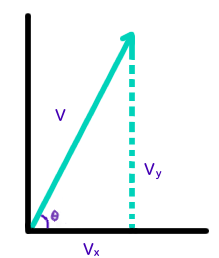
This diagram represents only one velocity vector, that is, the first (
We can see that
#color(purple)(v_y=vsin(theta))#
#=7/12"m"//"s"*sin(pi/8)#
#~~color(purple)(0.223" m"//"s")#
We can now make use of the above kinematic equation and solve for the fly time.
#(v_f)_y=(v_i)_y+a_yDeltat#
#=>Deltat=(cancel(v_f)-v_i)/a#
#=(-0.223"m"//"s")/(-9.8"m"//"s"^2)#
#=color(purple)(0.0228"s")#
We can now put this time into a new equation to find
#Deltax=(v_i)_xDeltat+cancel(1/2a_xDeltat^2)#
#Deltax=(v_i)_xDeltat#
As above, we find the parallel component of the initial velocity using trigonometry. We get
#=(7/12"m"//"s")cos(pi/8)(0.0228"s")#
#=0.0123"m"#
#~~color(purple)(1.23"cm")#
- This is the object's horizontal displacement.
We can now find the vertical displacement using
#Deltay=v_(iy)Deltat+1/2a_y(Deltat)^2#
#=>Deltay=(0.223" m"//"s")(0.0228"s")+1/2(-9.81" m"//"s"^2)(0.0228"s")^2#
#=>Deltay=0.0025"m"#
#=>color(purple)(=2.5"mm")#
For an overall displacement, we have:
#Deltas=sqrt((Deltax)^2+(Deltay)^2)#
#=>Deltas=sqrt((0.0123"m")^2+(0.0025"m")^2)#
#=>=0.0126"m"#
#=>~~color(purple)(1.26"cm")# .