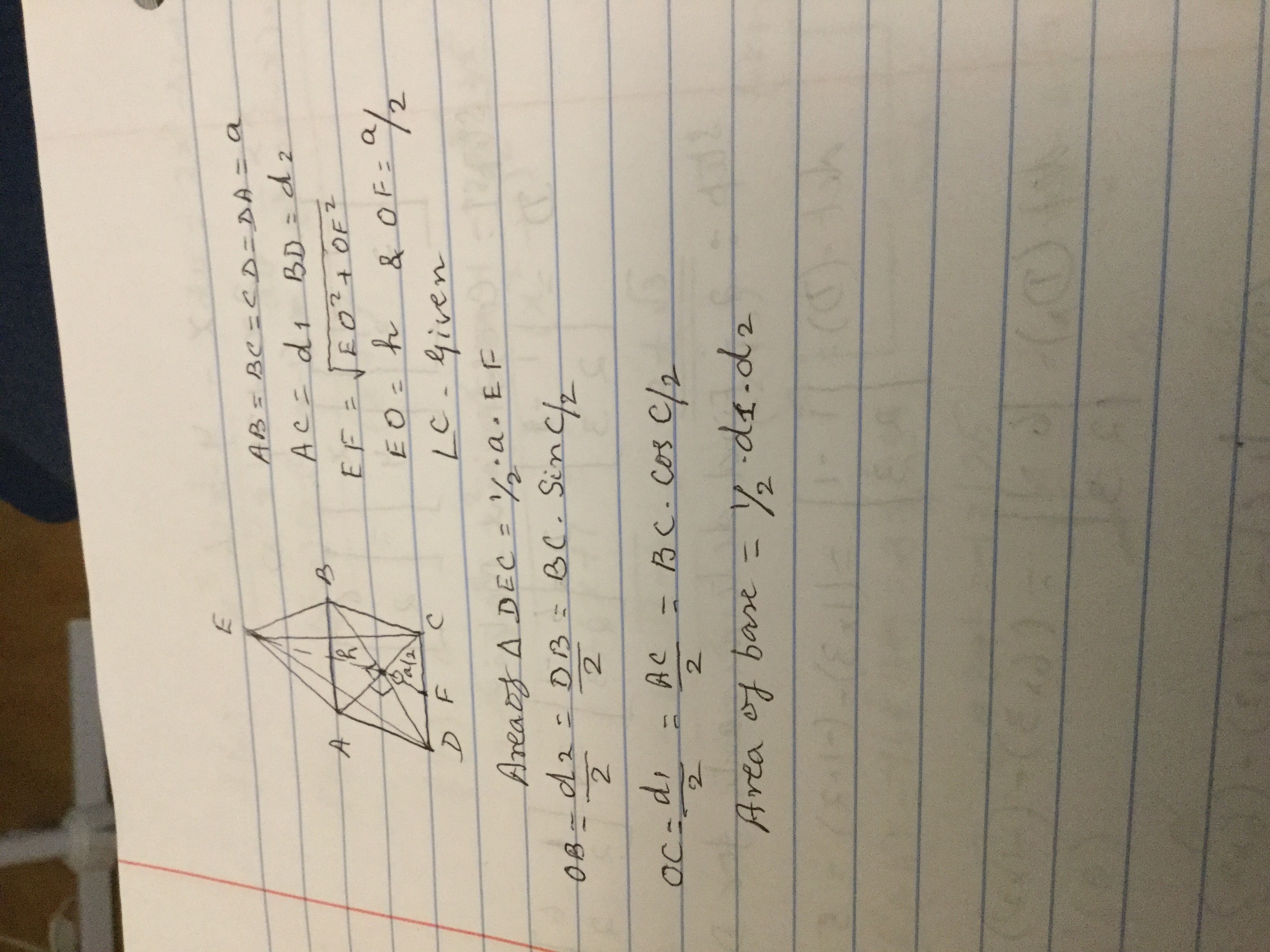Question

A pyramid has a base in the shape of a rhombus and a peak directly above the base's center. The pyramid's height is `9`, its base's sides have lengths of `4`, and its base has a corner with an angle of `(5 pi)/6`. What is the pyramid's surface area?

Answer 1

Total Surface Area `= **85.7944**`

Explanation:

AB = BC = CD = DA = a = 4
Height OE = h = 9
OF = a/2 = 2
`EF = sqrt(EO^2+ OF^2) = sqrt (h^2 + (a/2)^2) = sqrt(9^2+2^2)=sqrt85`

Area of `DCE = (1/2)*a*EF = (1/2)*4 *sqrt95 = 19.4936`
Lateral surface area `= 4*Delta DCE = 4*19.4936 = 77.9744`

`/_C = (5pi)/6, /_C/2 = (5pi)/12`
diagonal `AC = d_1` & diagonal `BD = d_2`
`OB = d_2/2 = BC*sin (C/2)=4*sin((5pi)/12) = 3.8637`
`OC = d_1/2 = BC cos (C/2) = 4* cos ((5pi)/12) = 1.0353`

Area of base ABCD `= (1/2)*d_1*d_2 = (1/2)(2*3.8637)(2*1.0353) = 8`

Total Surface Area #= Lateral surface area + Base area. T S A # 77.7944 + 8 = 85.7944#