A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of 3 and 2 and the pyramid's height is 9 . If one of the base's corners has an angle of (5pi)/12, what is the pyramid's surface area?
1 Answer
Apr 6, 2018
Explanation:
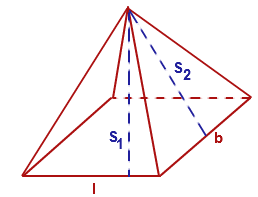 https://socratic.org/questions/a-pyramid-has-a-parallelogram-shaped-base-and-a-peak-directly-above-its-center-i-95
https://socratic.org/questions/a-pyramid-has-a-parallelogram-shaped-base-and-a-peak-directly-above-its-center-i-95
