A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of $3$ $3$ and $2$ $2$ and the pyramid's height is $3$ $3$ . If one of the base's corners has an angle of $\frac{π}{4}$ $pi/4$ , what is the pyramid's surface area?

Question

A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of $3$ $3$ and $2$ $2$ and the pyramid's height is $3$ $3$ . If one of the base's corners has an angle of $\frac{π}{4}$ $pi/4$ , what is the pyramid's surface area?

1 Answer

Impact of this question

1289 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-08T04:33:47

$T S A = L S A + A_{b a s e} = 19.98 + 4.24 = 24.22$ $color(indigo)(T S A = L S A + A_(base) = 19.98 + 4.24 = 24.22$ sq units

Explanation:

![https://socratic.org/questions/a-pyramid-has-a-parallelogram-shaped-base-and-a-peak-directly-above-its-center-i-123]( useruploads.socratic.org )

$Total Surface Area of Pyramid T S A = L S A + A_{b a s e}$ $"Total Surface Area of Pyramid " T S A = L S A + A_(base)$

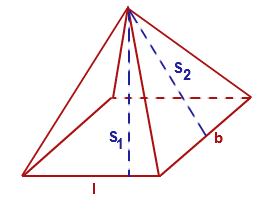
$l = 3, b = 2, θ = \frac{π}{4}, h = 3$ $l = 3, b = 2, theta = pi/4, h = 3$

$S_{1} = \sqrt{h^{2} + {(\frac{b}{2})}^{2}} = \sqrt{3^{2} + 1^{2}} = \sqrt{10} = 3.16$ $S_1 = sqrt (h^2 + (b/2)^2) = sqrt(3^2 + 1^2) = sqrt 10 = 3.16$

$S_{2} = \sqrt{h^{2} + {(\frac{l}{2})}^{2}} = \sqrt{3^{2} + {(1.5)}^{2}} = \sqrt{11.25} = 3.5$ $S_2 = sqrt (h^2 + (l/2)^2) = sqrt(3^2 + (1.5)^2) = sqrt (11.25) = 3.5$

$L S A = 2 ((\frac{1}{2}) l \cdot S_{1} + (\frac{1}{2}) b \cdot S_{2}) = l \cdot S_{1} + b \cdot S_{2}$ $L S A = 2((1/2) l * S_1 + (1/2) b * S_2) = l*S_1 + b*S_2$

$L S A = 3 \cdot 3.16 + 3 + 3.5 = 19.98$ $L S A = 3 * 3.16 + 3 + 3.5 = 19.98$

$A_{b a s e} = l b sin θ = 3 \cdot 2 \cdot (\frac{1}{\sqrt{2}}) = 3 \sqrt{2} = 4.24$ $A_(base) = l b sin theta = 3 * 2 * (1/sqrt2) = 3 sqrt2 = 4.24$

$T S A = L S A + A_{b a s e} = 19.98 + 4.24 = 24.22$ $color(indigo)(T S A = L S A + A_(base) = 19.98 + 4.24 = 24.22$ sq units

Science

Math

Humanities

... and beyond

A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of $3$ $3$ and $2$ $2$ and the pyramid's height is $3$ $3$ . If one of the base's corners has an angle of $\frac{π}{4}$ $pi/4$ , what is the pyramid's surface area?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of 3 33 and 2 22 and the pyramid's height is 3 33 . If one of the base's corners has an angle of pi/4 π4pi/4 , what is the pyramid's surface area?

1 Answer

Explanation:

Related questions

Impact of this question

A pyramid has a parallelogram shaped base and a peak directly above its center. Its base's sides have lengths of $3$ $3$ and $2$ $2$ and the pyramid's height is $3$ $3$ . If one of the base's corners has an angle of $\frac{π}{4}$ $pi/4$ , what is the pyramid's surface area?