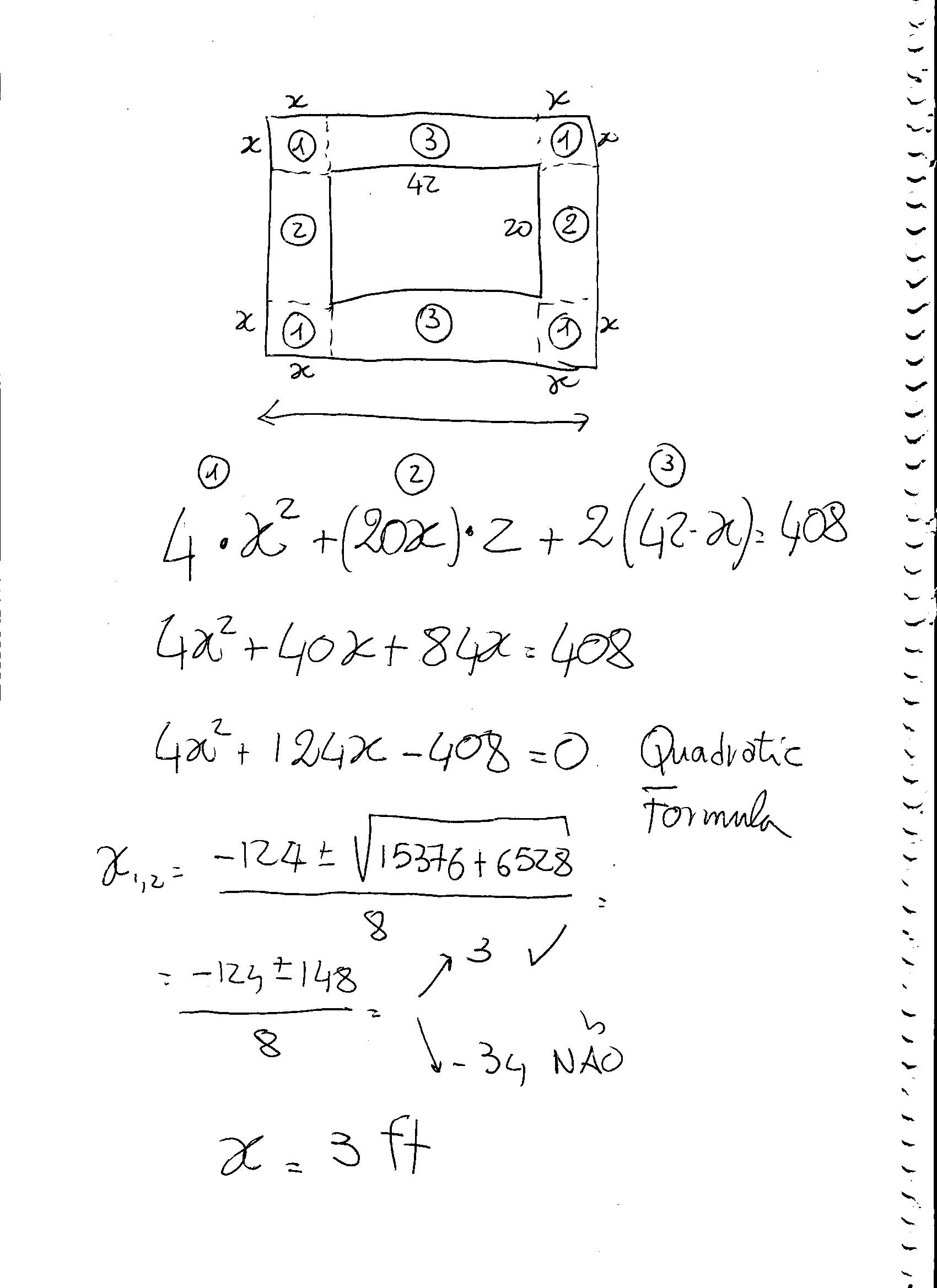
A rectangular garden 42 by 20 feet is surrounded by a walk way of uniform width. If the total area of the garden and walkway is 1248 square feet, what is the the width of the walkway?
2 Answers
Sep 10, 2015
I found
Explanation:
You can take the total area
So:
Sep 10, 2015
The walkway is
Explanation:
Define
Area of garden (including walkway)
With some basic algebra and arithmetic:
and (since the width can't be a negative number)

