A rifle that shoots bullets at is to be aimed at 460m/s a target 45.7 m away. If the center of the target is level with the rifle, how high above the target must the rifle barrel be pointed so that the bullet hits dead center?
1 Answer
Explanation:
The situation looks like this:
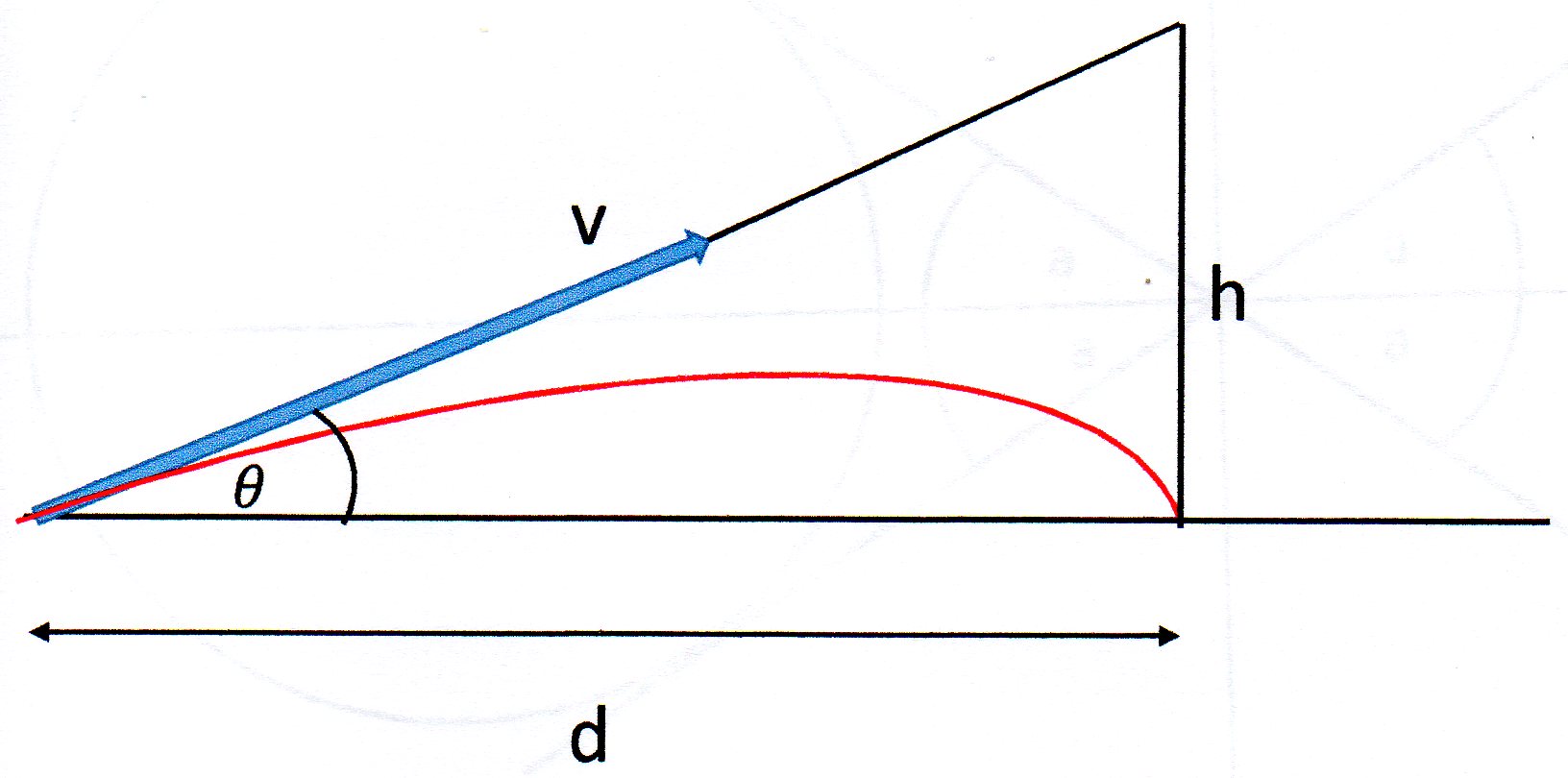
The mission here is to find
The range is given by:
- assuming level ground
Now looking at the diagram we can say that:
So the rifle should be pointed at
Addendum:
I have been asked to give the derivation for the range so here it is for anyone interested:
The key to these trajectory type questions is to treat the horizontal and vertical components of the motion separately and use the fact that they share the same time of flight.
The horizontal component of velocity is constant so we can write:
For the vertical component we can use the equation of motion
This becomes:
Substitute this into
Now we can put
There is a standard trig identity which states:
So substituting this into the expression for
So there you go.

