.
The formula for the curved surface area of a cone which does not include the area of the base is:
#A=pirl# where #r# is the radius of the base and #l# is the lateral height (slant height) as shown in yellow below:
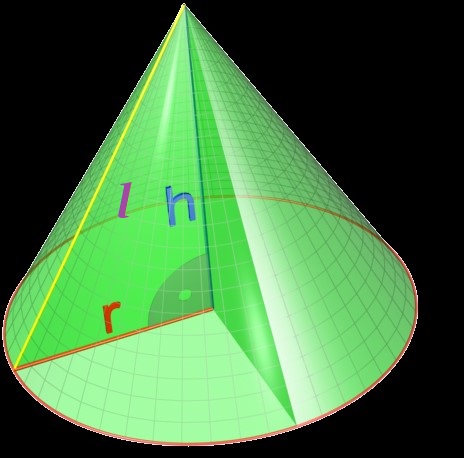
From the right angle triangle shown, using Pythagoras' formule, we get:
#l^2=h^2+r^2#
#l=sqrt(h^2+r^2#
Therefore, the curved area #A# is:
#A=pirsqrt(h^2+r^2)#
The volume formula is:
#V=1/3pir^2h#
Let's solve for #h# from the area formula and substitute it into the volume formula:
#A^2=pi^2r^2(h^2+r^2)#
#A^2=pi^2r^2h^2+pi^2r^4#
#pi^2r^2h^2=A^2-pi^2r^4#
#h^2=(A^2-pi^2r^4)/(pi^2r^2)#
#h=sqrt(A^2-pi^2r^4)/(pir)#
#V=1/3pir^2sqrt(A^2-pi^2r^4)/(pir)#
#V=1/3rsqrt(A^2-pi^2r^4)=1/3r(A^2-pi^2r^4)^(1/2)#
To find the maximum volume, we take the derivative of the volume function and set it equal to #0#:
#(dV)/(dr)=1/3[r(1/2)(A^2-pi^2r^4)^(-1/2)(-4pi^2r^3)+(A^2-pi^2r^4)^(1/2)]#
#(dV)/(dr)=1/3((-2pi^2r^4)/sqrt(A^2-pi^2r^4)+sqrt(A^2-pi^2r^4))#
#(dV)/(dr)=(-2pi^2r^4+A^2-pi^2r^4)/(3sqrt(A^2-pi^2r^4)#
#(dV)/(dr)=(-3pi^2r^4+A^2)/(3sqrt(A^2-pi^2r^4))=0#
#-3pi^2r^4+A^2=0#
#A^2=3pi^2r^4#
Let's substitute for #A# from the area formula:
#pi^2r^2(h^2+r^2)=3pi^2r^4#
Dividing both sides by #pi^2r^2#, we get:
#h^2+r^2=3r^2#
#h^2=2r^2#
#h^2/r^2=2#
#h/r=sqrt2/1#


