Question

A rod of length `f/2` is placed along the axis of a concave mirror of focal length `f`.IF the near end of the REAL IMAGE formed by the rod just touches the far end of the ROD,what is its magnification?

dont get confused ,question is absolutely correct,and read it twice,ans anyways.

Answer 1

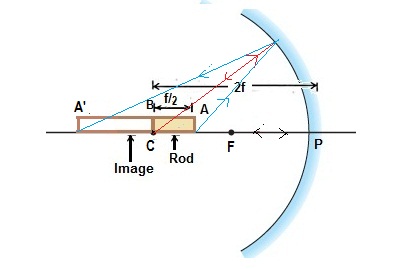
A rod AB of length `f/2` is placed along the axis of a concave mirror of focal length `f` in such a way that the near end of the REAL IMAGE formed by the rod just touches the far end B of the ROD.
The near end of the real image of the rod is the image of far end B of the the rod AB. It is possible only if the far end B of the rod is placed at the center of curvature C of the concave mirror (as shown in the figure).
The image of near end A of the rod is A'

Now PC = the radius of curvature `=2f`

The object distance for near point of the rod A is `u`

So `u=PA=PC-AB=2f-f/2=(3f)/2`

The conjugate foci relation of spherical mirror is

`1/v+1/u=1/f......(1)`

Where

`v->"Image distance"=?`

`u->"Object distance"=-(3f)/2`

`f->"Focal length"=-f`

So inserting the values in equation (1)

`1/v-2/(3f)=-1/f`

`=>1/v=-1/f+2/(3f)`

`=>1/v=(-3+2)/(3f)=-1/(3f)`

`=>v=-3f`
Negative sign indicates the position of image point A' is at the same side of object point A

So length/size of the image

`BA'=CA'=PA'-PC=3f-2f=f`

Now Magnification

`m="Size of image"/"Size of object"=f/(f/2)=2`