A sample of compound containing C, O, and silver (Ag) weighed 1.372 g. On analysis it was found to contain 0.288 g O and 0.974 g Ag. The molar mass of the compound is 303.8 g/ mol. What is the empirical and molecular formula of the compound?
First in order to do the empirical formula I need to find moles but in the question I dont have the mass of carbon in the compound. So I added the mass of oxygen and Ag and then subtracted from the mass of the total compound and got .11 grams
I then began to find the moles of each atom in the compound
so for oxygen
(0.288 grams oxygen) (1 mole Oxygen/ 16.00 grams ) = .018 moles O
For carbon
(.11 grams carbon) (1mole carbon / 12.01 grams) =.0090268767 moles C
For Silver
(0.974 g Ag) (1 mole Ag / 107.9 g) = .0090268767 moles Ag
Then I went to find the ratio relationship of the element of the compound and figured that silver was the smallest so i divided the moles with that amount
Oxygen
(.018/.0090268767) = 1.99 so I rounded to 2
carbon
(.0091590341/.0090268767) = 1.01 rounded to 1
Ag
(.0090268767/.0090268767) = 1
So I concluded the empirical formula is
AgCO2
for the molecular formula the problem gave me the molar mass is 303.8 g/ mol so i did the molar mass of the empircal formula and had 303.8 divided by the molar mass of the empirical formula
((303g/mol))/((147.92g/mol)) = 2 empirical units
so the molecular formula is
AG2C2O4
NOW my question is
is there a way to check if these two are the correct answers? I want to know if these are correct
First in order to do the empirical formula I need to find moles but in the question I dont have the mass of carbon in the compound. So I added the mass of oxygen and Ag and then subtracted from the mass of the total compound and got .11 grams
I then began to find the moles of each atom in the compound
so for oxygen
(0.288 grams oxygen) (1 mole Oxygen/ 16.00 grams ) = .018 moles O
For carbon
(.11 grams carbon) (1mole carbon / 12.01 grams) =.0090268767 moles C
For Silver
(0.974 g Ag) (1 mole Ag / 107.9 g) = .0090268767 moles Ag
Then I went to find the ratio relationship of the element of the compound and figured that silver was the smallest so i divided the moles with that amount
Oxygen
(.018/.0090268767) = 1.99 so I rounded to 2
carbon
(.0091590341/.0090268767) = 1.01 rounded to 1
Ag
(.0090268767/.0090268767) = 1
So I concluded the empirical formula is
AgCO2
for the molecular formula the problem gave me the molar mass is 303.8 g/ mol so i did the molar mass of the empircal formula and had 303.8 divided by the molar mass of the empirical formula
((303g/mol))/((147.92g/mol)) = 2 empirical units
so the molecular formula is
AG2C2O4
NOW my question is
is there a way to check if these two are the correct answers? I want to know if these are correct
1 Answer
Yes, your answer is correct.
Explanation:
That is exactly the approach to have when dealing with this type of problems.
-
find the mass of the third element by using the total mass of the sample
-
use the molar masses of the constituent elements to determine how many moles of each you have in that sample
-
find the mole ratios that exist between the elements by dividing all the values you got for the number of moles by the smallest one
-
make sure that this mole ratio is the smallest whole number ratio that can exist
-
use the molar mass of the empirical formula to find the molecular formula
You can always test your result by looking at the compound's chemical formula.
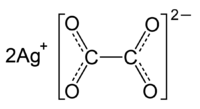
In this case,
As you can see from the charges, you'd need two silver cations to balance the
ALTERNATIVE APPROACH
Here's how you could use the information given to you to find the molecular formula first, then backtrack and find the empirical formula.
Use the molar mass of the compound to determine how many moles you have in that
#1.372 color(red)(cancel(color(black)("g"))) * "1 mole"/(303.8color(red)(cancel(color(black)("g")))) = "0.004516 moles"#
Now use the molar masses of the three elements to find how many moles of each you get in the sample
#"For C: " 0.11 color(red)(cancel(color(black)("g"))) * "1 mole C"/(12.011color(red)(cancel(color(black)("g")))) = "0.009158 moles C"#
#"For O: " 0.288color(red)(cancel(color(black)("g"))) * "1 mole O"/(15.9994color(red)(cancel(color(black)("g")))) = "0.01800 moles O"#
#"For Ag: " 0.974color(red)(cancel(color(black)("g"))) * "1 mole Ag"/(107.87color(red)(cancel(color(black)("g")))) = "0.009030 moles Ag"#
At this point, you can calculate exactly how many moles of each element you get in one mole of this unknown compound by using the number of moles as a conversion factor.
You will have
#1 color(red)(cancel(color(black)("mole compound"))) * "0.009158 moles C"/(0.004516color(red)(cancel(color(black)("moles compound")))) = 2.03 ~~ "2 moles C"#
#1color(red)(cancel(color(black)("mole compound"))) * "0.01800 moles O"/(0.004516color(red)(cancel(color(black)("moles compound")))) = 3.99 ~~ "4 moles O"#
#1color(red)(cancel(color(black)("mole compound"))) * "0.009030 moles Ag"/(0.004516color(red)(cancel(color(black)("moles compound")))) = "2 moles Ag"#
Since this is how many moles of each element you get in one mole of compound, you can say that the molecular formula will be
#color(green)(|bar(ul(color(white)(a/a)"Ag"_2"C"_2"O"_4color(white)(a/a)|))) -># molecular formula
To get the empirical formula, rewrite the ratio
#color(green)(|bar(ul(color(white)(a/a)"Ag"_1"C"_1"O"_2 implies "AgCO"_2color(white)(a/a)|))) -># empirical formula
And there you have it, two approaches that you can use to double-check your result.