Question

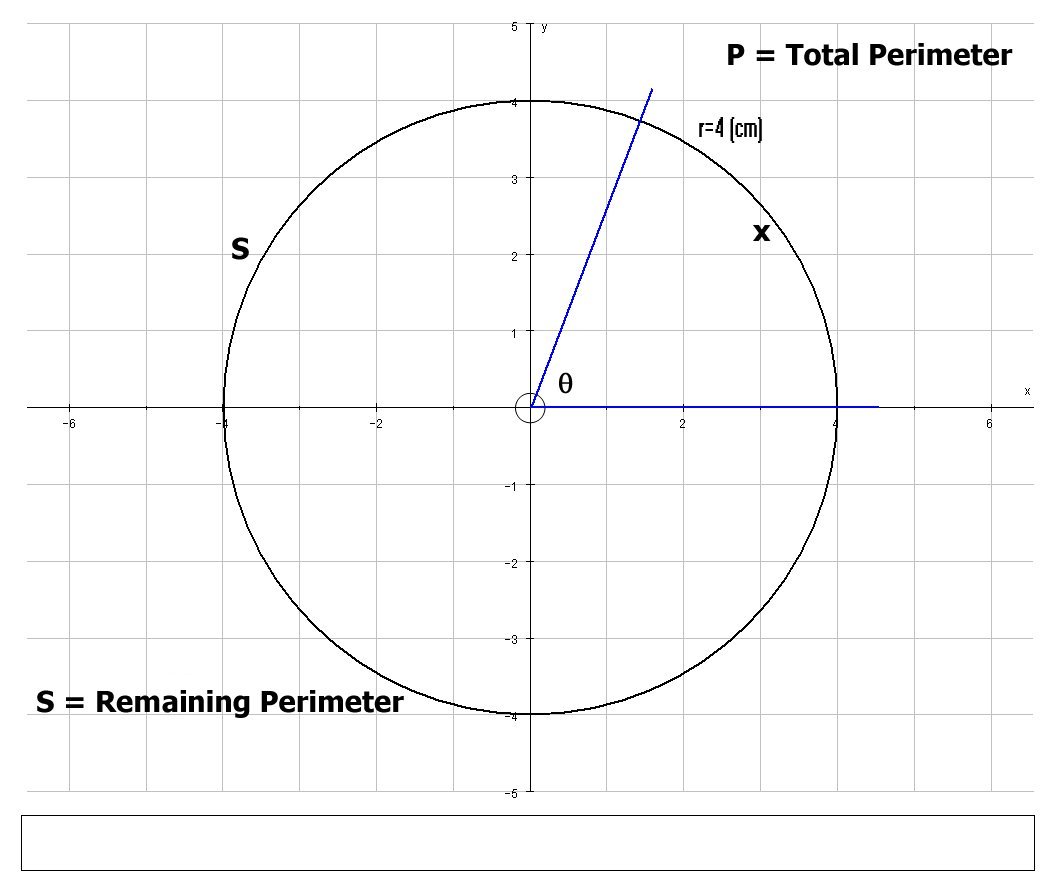
A sector of arc length x cm is removed from a circular piece of paper of radius 4 cm. The remaining piece is used to make a cone. Find x so that the volume of the cone is a maximum?

Answer 1

`x = (24-8sqrt(6)pi)/3 ~~ 4.61194394612852 \ cm`

Explanation:

Let us define the following variables:

# { (P,"arc-length of the entire circle", cm), (x,"arc-length of the sector removed", cm), (S, "arc-length of remaining 'pac-man' shape", cm), (r, "radius of the newly formed cone", cm), (l, "slant length of the newly formed cone", cm), (h, "height of the newly formed cone", cm), (V, "Volume of the newly formed cone", cm^3) :} #

Using the standard equation for the perimeter of a circle `(P=2pir)`

`P = (2pi)(4) = 8pi`

And, we also have:

`x+S = P => S = 8pi-x`

This remaining arc length, `S` will then become the circumference of the newly formed cone. Again using `P=2pir`, we have:

`S = 2pir => 8pi-x = 2pir`
`:. r = 4 - x/(2pi)`

We can now compute the height of the newly formed cone, as the cone will have radius `r`, and its slant `l` will be `4 \ cm`, and so by Pythagoras:

`l^2 = h^2 + r^2`

`:. 4^2 = h^2 + (4 - x/(2pi))^2`
`:. h^2 = 16 - (16-(4x)/pi+x^2/(4pi^2) )`
`:. h = sqrt((4x)/pi-x^2/(4pi^2) )`

Now, using the standard formula, `V=1/3pir^2h`, for the volume of a cone, we have:

`V = pi/3(4 - x/(2pi))^2 sqrt((4x)/pi-x^2/(4pi^2) )`

We seek a critical point of this computed volume function wrt `V`. For simplicity, consider:

`V^2 = pi/3(4 - x/(2pi))^2 sqrt((4x)/pi-x^2/(4pi^2) ))^2`

`\ \ \ \ = pi^2/9(4 - x/(2pi))^4 ((4x)/pi-x^2/(4pi^2) )`

`\ \ \ \ = pi^2/9((8pi - x)/(2pi))^4 ( (16pix-x^2)/(4pi^2) )`

`\ \ \ \ = pi^2/9 * 1/(16pi^4) (8pi - x)^4 1/(4pi^2) (16pix-x^2)`

`\ \ \ \ = 1/(575pi^4) (8pi - x)^4 (16pix-x^2)`

And now we can differentiate (implicitly) wrt `x` using the product rule to get:

`2V(dV)/dx = 1/(575pi^4) { (8pi - x)^4 (16pi-2x) + 4(8pi-x)^3(-1)(16pix-x^2) }`

At a critical point we require that this derivative vanish, ie, `(dV)/dx = 0`:

`:. (8pi - x)^4 (16pi-2x) - 4(8pi-x)^3(16pix-x^2) = 0`
`:. (8pi - x)^3( (8pi - x)(16pi-2x) - 4(16pix-x^2)) = 0`
`:. 2(8pi - x)^3( (8pi - x)(8pi-x) - 2(16pix-x^2)) = 0`
`:. 2(8pi - x)^3(3x^2 - 48pix + 64pi^2) = 0`

Which has solutions given by:

`(8pi-x) = 0 => x=8pi ~~ 25.13 \ cm`
`(3x^2 - 48pix + 64pi^2) = 0 => x=(8+-8sqrt(2/3))pi`

Initially, In order for a sector of acr-length `x` to be removed we require that `x lt P => x lt 8pi` so we can reject all but one solution giving us:

`x = ((24 - 8sqrt(6))pi)/3 ~~ 4.61194394612852 \ cm`

And if we check the graph of the volume function we can readily validate that this value of `x` is consistent with our findings, and indeed corresponds to a maximum of the volume:
graph{1/3pi(4 - x/(2pi))^2 (sqrt((4x)/pi-x^2/(4pi^2) )) [-5, 10, -5, 40]}