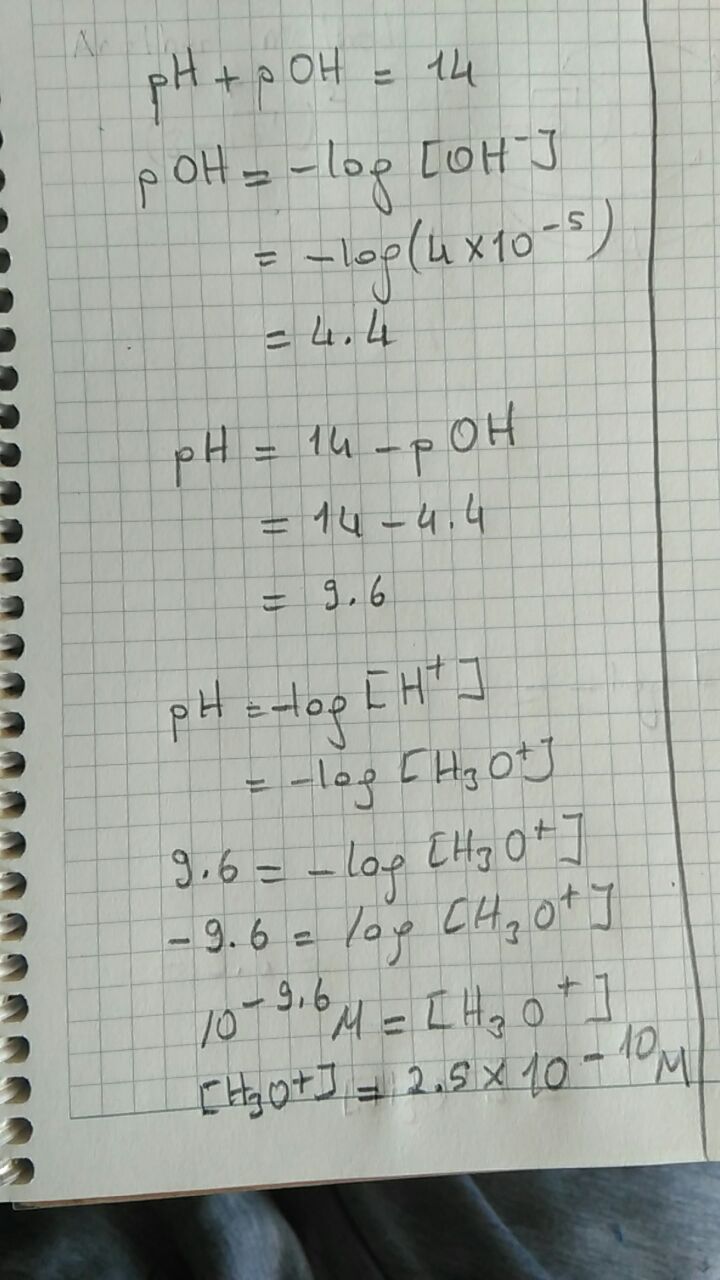A solution contains #[OH^-] = 4.0 times 10^-5# #M#, what is the concentration of #[H_3O^+]#?
3 Answers
May 25, 2017
Explanation:
In aqueous solution, it is a fact that the following equilibrium operates under standard conditions.........
Under standard conditions............
So
And thus
May 25, 2017
Explanation:
Given that no hydrolysis happened in the solution (inferred from question) Calculate