A street light is at the top of a 15 foot tall pole. A 6 foot tall woman walks away from the pole with a speed of 4 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 50 feet from the base of the pole?
1 Answer
May 10, 2018
Explanation:
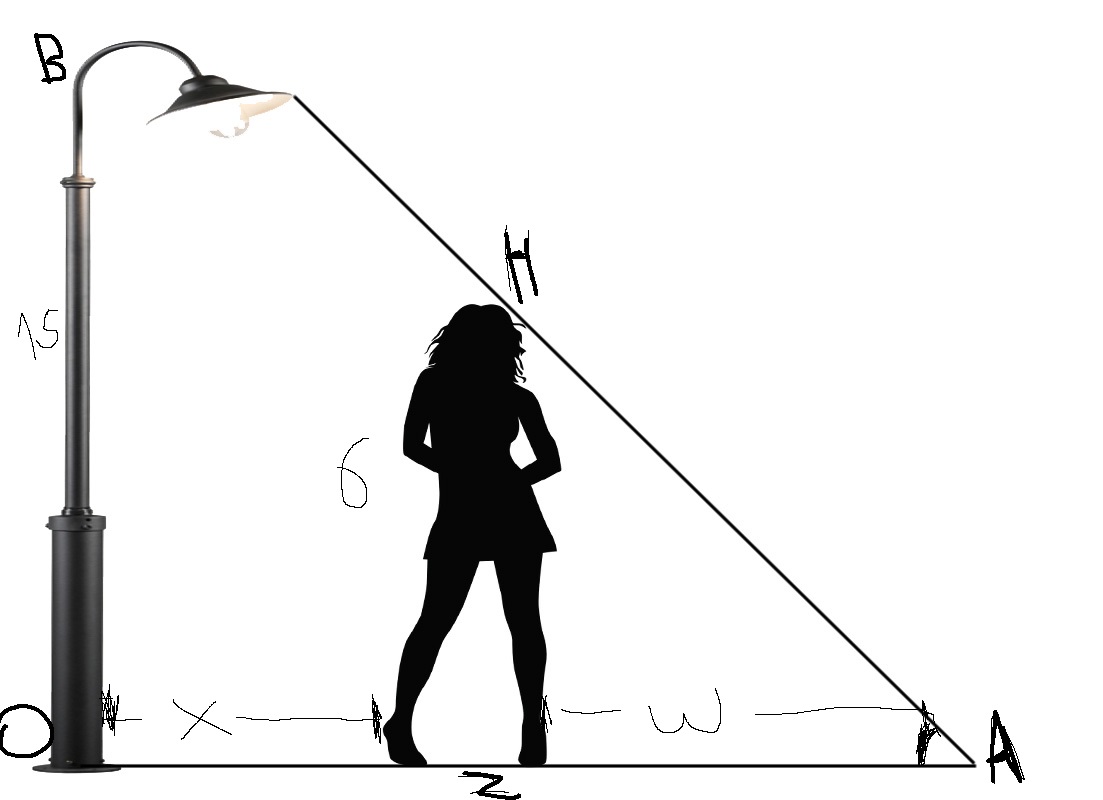
Using Thales Proportionality theorem for the triangles
The triangles are similar because they have
We have
Let
-
d(t)=(5x(t))/3 -
d'(t)=(5x'(t))/3
For
Therefore,

