A student used 0.1611 g of aluminum with excess HCl. This produced 205.1 mL of hydrogen gas. Atmospheric pressure was 754.7 torr and room temperature that day was 20.5 degrees Celsius?
Please help I am having a hard time. Can you please show all steps....
How many moles of hydrogen were produced?
What was the vapor pressure of the water at that temperature in torr?
What was the partial pressure of hydrogen in atm?
What value of R did the student obtain in L atm mol-1 K-1?
Please help I am having a hard time. Can you please show all steps....
How many moles of hydrogen were produced?
What was the vapor pressure of the water at that temperature in torr?
What was the partial pressure of hydrogen in atm?
What value of R did the student obtain in L atm mol-1 K-1?
1 Answer
Warning! Long Answer. Here's what I get.
Explanation:
It appears that you were collecting the hydrogen over water.
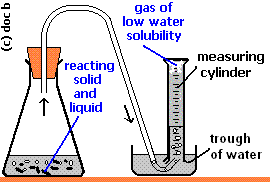
Then, the gas you collected was a mixture of hydrogen and water vapour.
When you equalized the water levels inside the trough and the measuring cylinder, the total pressure of the two gases equalled the atmospheric pressure.
#p_text(atm) = p_text(H₂) + p_text(H₂O)#
There is no way that you could calculate the partial pressure of the water. Your instructor would either have given you the number or directed you to a table of vapour pressures like the one here.
Here's part of the table.
You interpolate between the two pressures to get the pressure at 20.5 °C.
∴
and
In atmospheres
We can use the Ideal Gas Law to calculate the moles of
#color(blue)(bar(ul(|color(white)(a/a)pV = nRTcolor(white)(a/a)|)))" "#
We can rearrange this formula to get
#n = (pV)/(RT)#
You need the value of
Your instructor would either have given you the value or told you to look it up your text.
In this problem,
∴
You collected

