A substance in an aqueous solution at a concentration of 0.01M shows an optical transmittance of 28% with a path length of 2mm calculate the molar absorption coefficient of the solute? What would be the transmittance in a cell of 1cm thick?
1 Answer
(a)
Explanation:
The absorption of radiation
Many compounds absorb ultraviolet (UV) or visible (VIS) light as it passes through a solution.
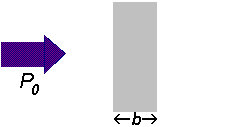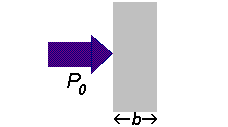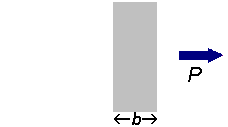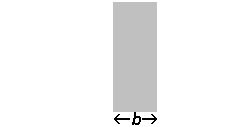
If a beam of radiation of power
We can express the amount of radiation absorbed as transmittance
#color(blue)(bar(ul(|color(white)(a/a)T = P/P_0color(white)(a/a)|)))" "#
We can express the amount of radiation absorbed as absorbance
#color(blue)(bar(ul(|color(white)(a/a)A = "-log"Tcolor(white)(a/a)|)))" "#
The Beer-Lambert Law
The Beer-Lambert Law states that the absorbance
#color(blue)(bar(ul(|color(white)(a/a)A = epsilonclcolor(white)(a/a)|)))" "#
Now, we can write
or
Part (a). Calculate the molar absorption coefficient
Part (b). Calculate the transmittance

