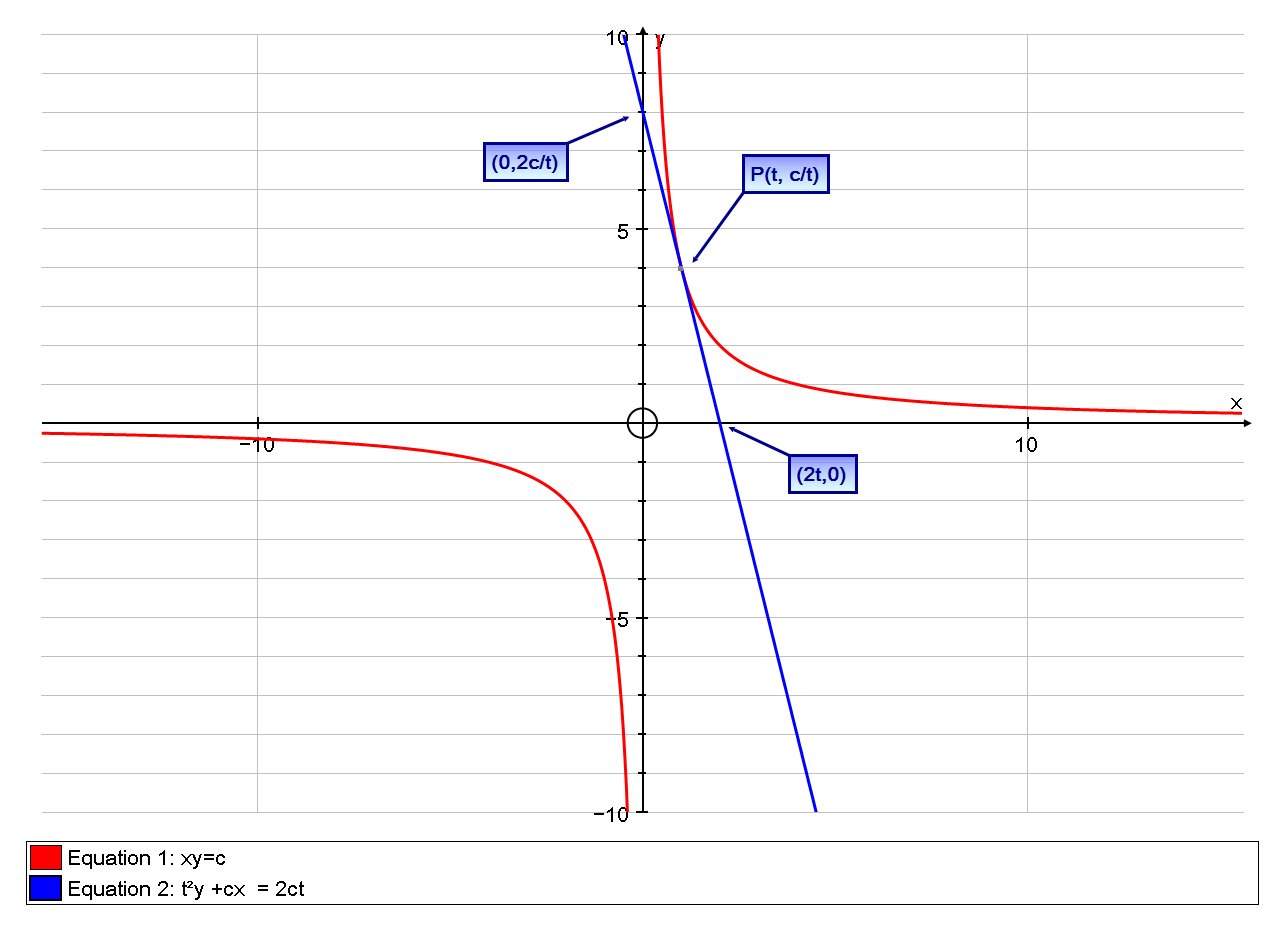
A tangent line is drawn to the hyperbola #xy=c# at a point P, how do you show that the midpoint of the line segment cut from this tangent line by the coordinate axes is P?
1 Answer
We have
Let us suppose that P has x-coordinates
So the gradient of the tangent at P is given by
when
The tangent passes through
Now Let's find the midpoint of the tangent line as its passes through the axis.
The tangent cuts the
The tangent cuts the
This yields two solutions:
1) Either,
#t=0# which corresponds to a vertical asymptote#(0,oo)# which we can dismiss as a valid solution
2) Or#ty-2c=0 => y=(2c)/t#
So the tangent touches the axis at
So the mid-pint of these two coordinates is: