Question

A tree casts a shadow 9.3.m long when the angle of the sun is 43°. How tall is the tree?

Answer 1

The tree is about `color(blue)("8.67 meters"` tall.

Explanation:

`" "`
Examine the image below:

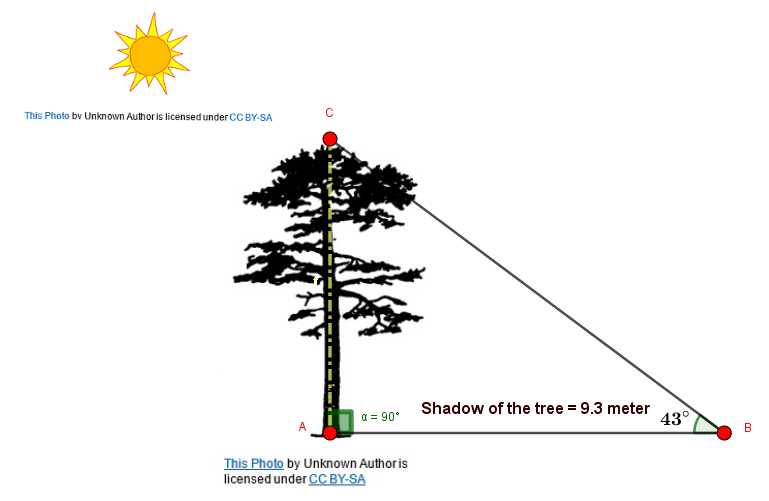
The tree's shadow (AB) is `"9.3 meters"` long.

From the location B, the sun is at an angle of is `43^@`.

Our objective is to find the height of the tree (AC)

We are given angle `43^@`.

Side opposite to this angle is `AC`, which is the height of the tree.

Side adjacent to this angle is `AB`

The formula which connects these three known values is:

`tan(/_ABC) =` Opposite Side`/` Adjacent Side.

`rArr tan(43^@) = (AB)/(BC)`

`:. AB = tan(43^@)*BC`

Using the calculator, `tan(43^@) ~~ 0.9325`

So,

`AB~~(0.9325)*(9.3)`

`AB~~8.67239` meters.

Hence, the tree is about `color(blue)("8.67 meters"` tall.

Hope you find this solution useful.