A triangle as corners at #(2 ,5 )#, #(7 ,2)#, and #(3 ,1)#. If the triangle is dilated by a factor of #4 # about #(1 ,9), how far will its centroid move?

Question

1001 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-10T02:11:03

Distance moved by centroid due to dilation factor 4 is

#color(green)(GG' ~~ 16.36)#

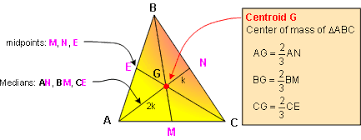
enter image source here

Centroid #G((x),(y)) -> (((2+7+3)/3),((5+2+1)/3) )=> ((4), (8/3))#

#color(blue)(G ((4),(8/3))#

Dilated about point D ((1),(9))# by a factor of 4

#vec(G'D) = 4 * vec(GD)#

#((x - 1),(y - 9)) = 4 * ((4-1),(8/3-9)) => 4 ((3),(-19/3))#

#x - 1 = 4 * 3 = 12, x = 13#

#y - 9 = 4 * (-19/3) = -76/3, y = 49/3#

#color(blue)(G'((13),(49/3))#

Distance moved by G to G'

#vec(GG' )= sqrt((13-4)^2 + (49/3 - 8/3)^2) ~~ color(brown)(16.36)#