Question

A triangle has corners at `(1, 3 )`, ( 2, -4)`, and`(8, -5 )#. If the triangle is reflected across the x-axis, what will its new centroid be?

Answer 1

New centroid `color(indigo)(G’(x, y) => ( 11/3, -2)`

Explanation:

Reflection rules

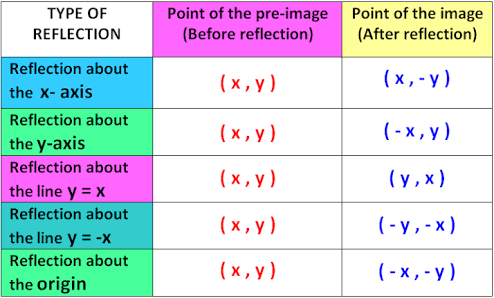
Reflection about the x - axis `color(red)(x,y) color(blue)(-> )color(purple)(x, -y)`

Three points A, B, C will become A’, B’, C’.

`color(red)(A ( 1, 3) ) color(blue)(- >) color(purple)( A’ (1, -3))`

`color(red)(B ( 2, -4) ) color(blue)(- >) color(purple)( B’ (2, 4))`

`color(red)(A ( 8, -5) ) color(blue)(- >) color(purple)( C’ (8, 5))`

New Centroid is found out using the formula


`color(green)G’_x = (x_A + x_B + x_C) / 3 = (1 + 2 + 8) / 3 = color(green)(11/3)`

`color(green)G’_y = (y_A + y_B + y_C) / 3 = (-3 + 4 + 5) / 3 = color(green)(2)`

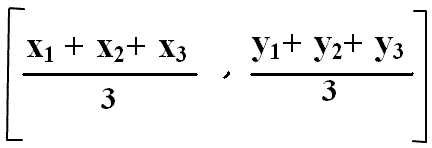
New centroid `color(indigo)(G’(x, y) => ( 11/3, -2)`