A triangle has corners at #(1 ,3 )#, #(9 ,4 )#, and #(2 ,2 )#. If the triangle is dilated by a factor of #2 # about point #(9 ,5 ), how far will its centroid move?
1 Answer
Jun 22, 2016
distance
Explanation:
Compute for the centroid
Centroid
Factor of 2 about the point
Let
Solve for
Solve for
The new centroid
Solve for the distance between the two centroids
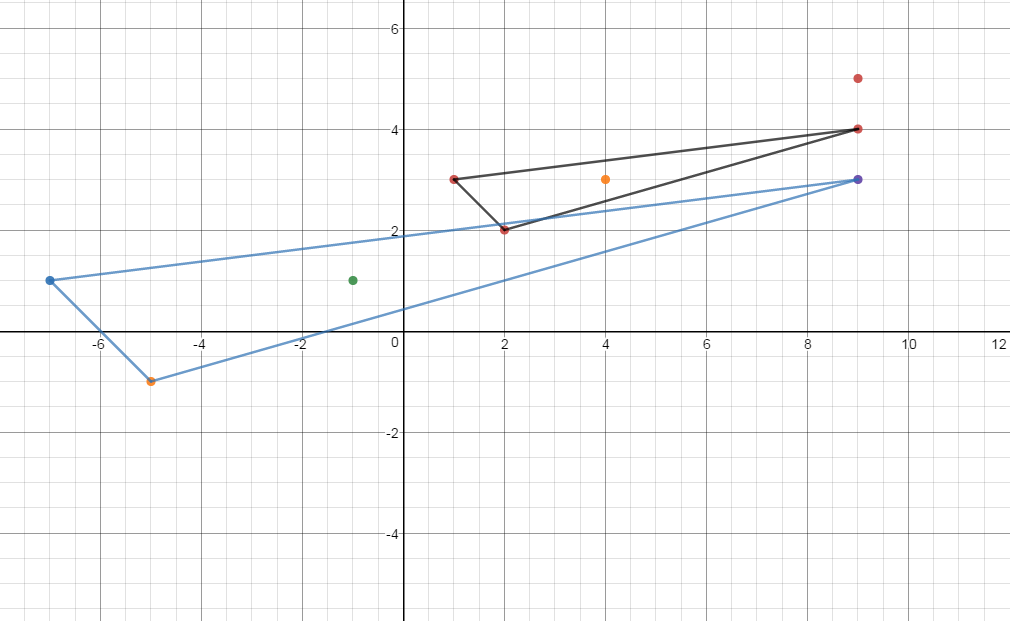
KIndly see the drawings of the old and new triangles
God bless....I hope the explanation is useful.
