A triangle has corners at #(1 ,4 )#, #(7 ,5 )#, and #(3 ,2 )#. How far is the triangle's centroid from the origin?
1 Answer
Jul 25, 2016
distance of centroid from origin is:
Explanation:
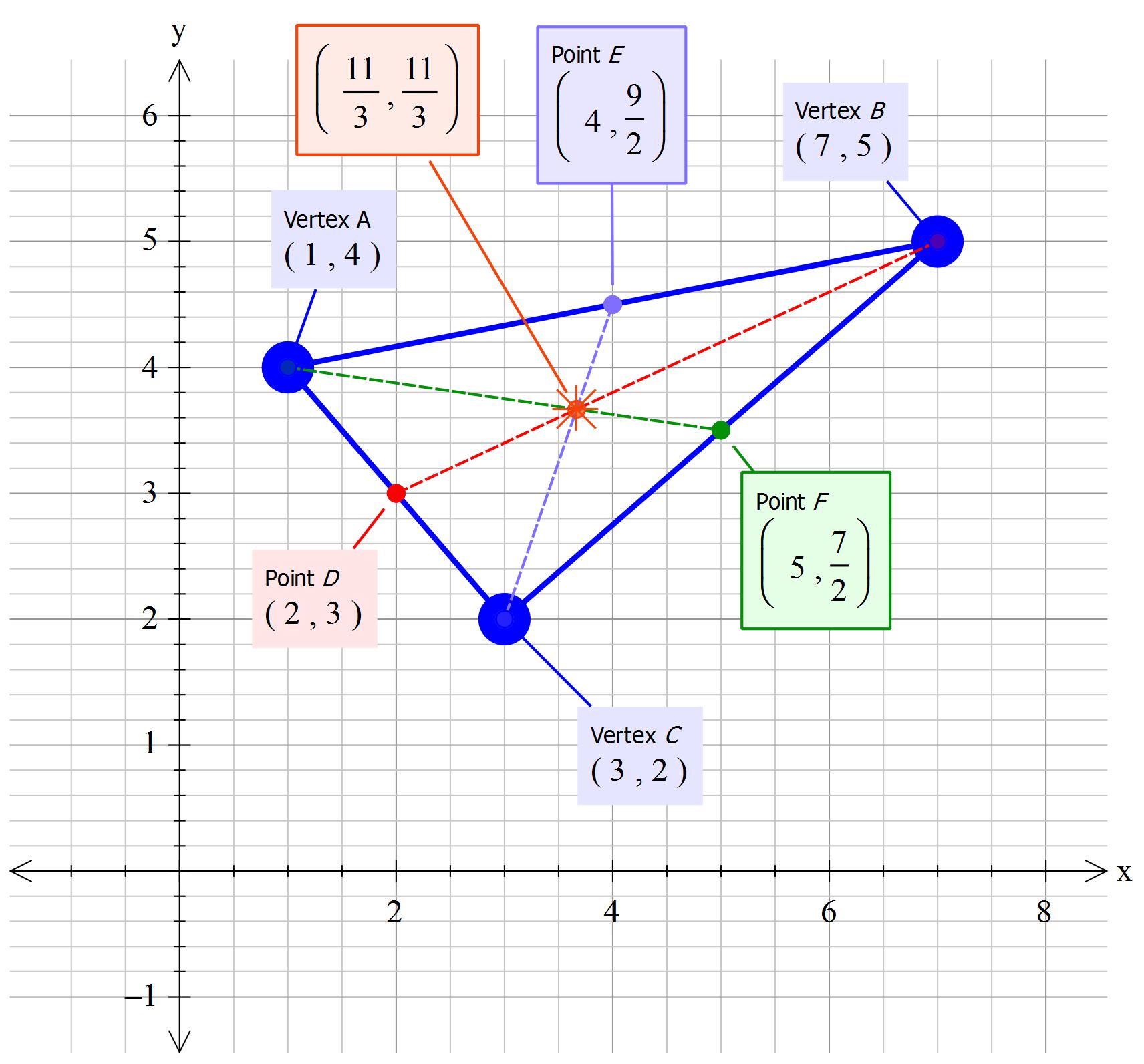
The triangle's centroid is the mean point.
So mean
Mean
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using Pythagoras
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

