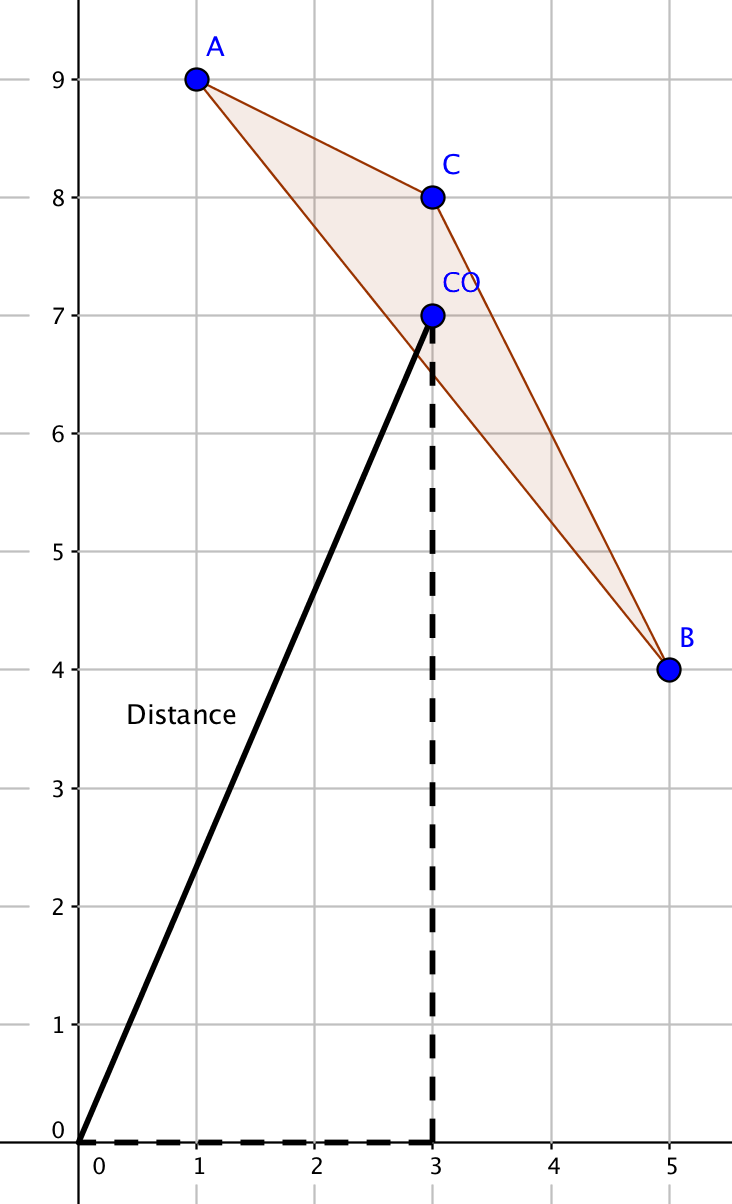
A triangle has corners at (1 ,9 ), (5 ,4 ), and (3 ,8 ). How far is the triangle's centroid from the origin?
1 Answer
Jun 18, 2016
It is
Explanation:
If
In our case
Then the centroid has coordinates