#"The original triangle and its centroid is shown in figure below."#
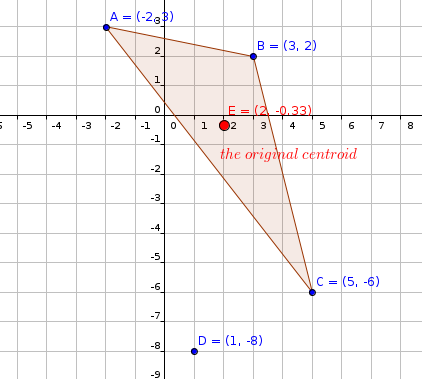
#"the original centroid can be calculated using:"#
#x=(-2+3+5)/3=6/3=2#
#y=(3+2+-6)/3=-1/3=-0,33#
#E(2,-0.33)#
#"Now dilate A(-2,3) by factor 2 with respect to D(1,-8)"#
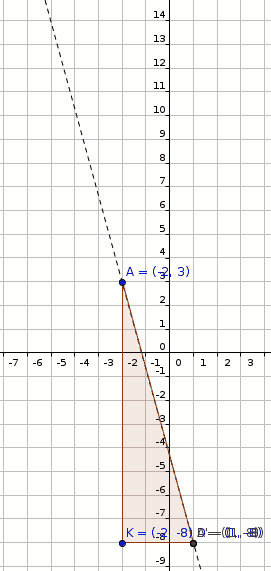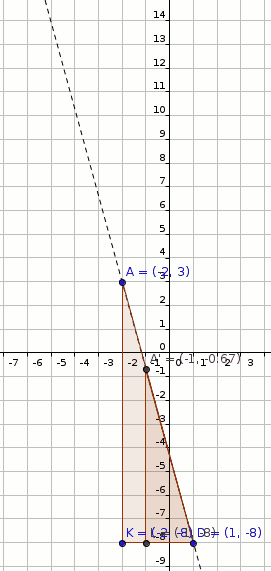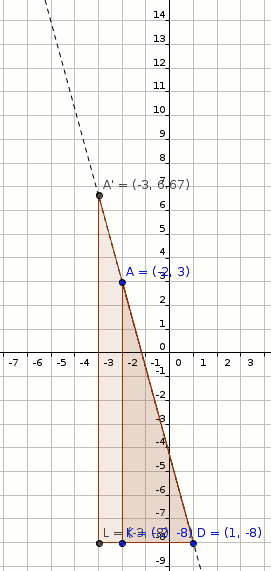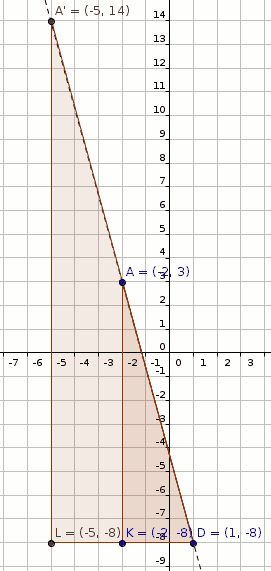
#A(-2,3) rArr A'(1-3*2,3+11*2)#
#A'(1-3*2,-8+11*2)#
#A'(-5,14)" (shown in figure below)"#
# #
#"Dilate B(3,2) by factor 2 with respect to D(1,-8)"#
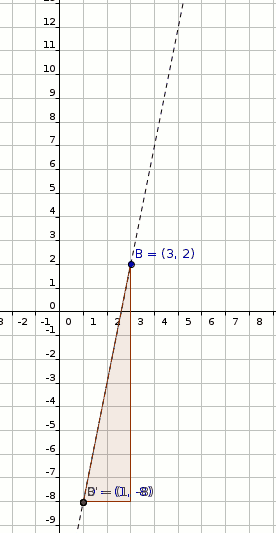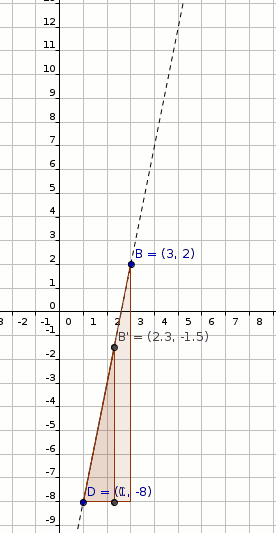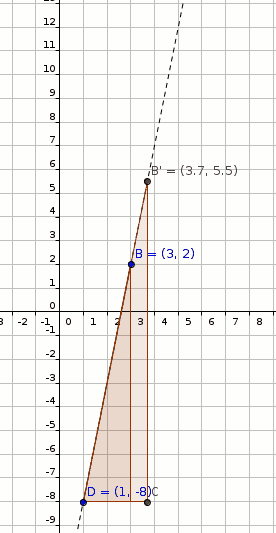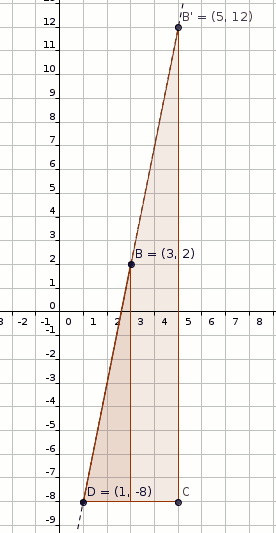
#B(3,2) rArr B'(1+2*2,-8+10*2)#
#B'(1+2*2,-8+10*2)#
#B'(5,12)" (shown in figure below)"#
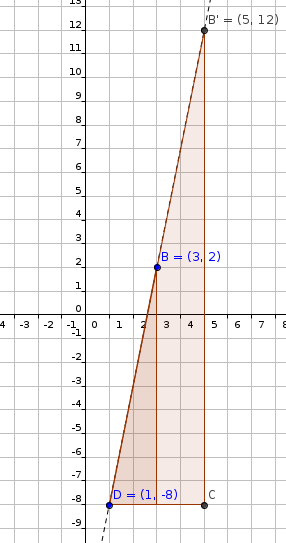
#"Dilate C(5,-6) by factor 2 with respect to D(1,-8)"#
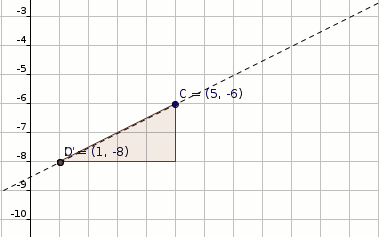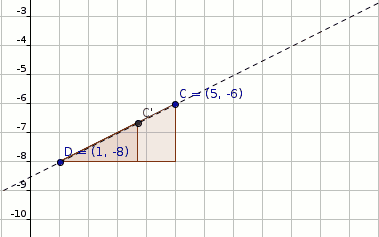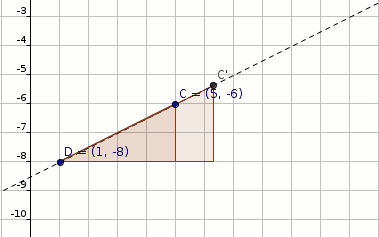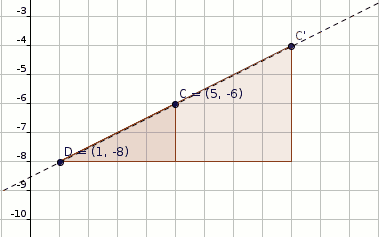
#C(5,-6) rArr C'(1+4*2,-8+2*2)#
#C'(1+4*2,-8+2*2)#
#C'(9,-4)" (shown figure below)"#
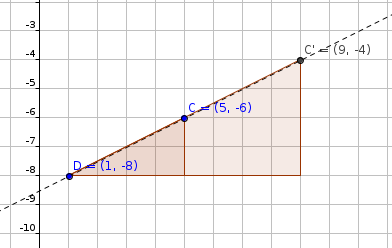
#"Finally.."#
#"the dilated centroid can be calculated " #
#x'=(-5+5+9)/3=9/3=3#
#y'=(14+12-4)/3#
#y'=22/3=7,33#
#F(3,7.33)#
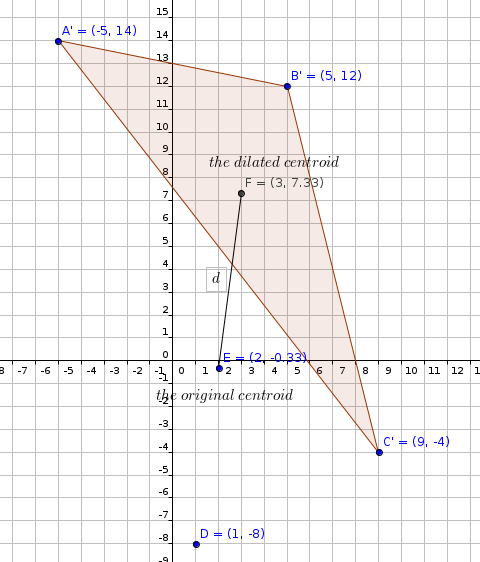
#"distance between E and F"#
#d=sqrt((3-2)^2+(7.33+0.33)^2)#
#d=sqrt(1+(7.66)^2)#
#d=sqrt(1+58.68)#
#d=sqrt(59.68)#
#d=7.73#













