A triangle has corners at #(2 , 6 )#, #(3 ,8 )#, and #(4 ,5 )#. What is the radius of the triangle's inscribed circle?

1 Answer
Cri007
Mar 26, 2017

See below.

Explanation:

Solution 1:
By the formula #A=rs#, where #A# is the area of the triangle, #r# is the radius of the inscribed circle, and #s# is the semi-perimeter of the triangle, if we know the area and the semi-perimeter, we can find the radius.

To find the area, we use Shoelace.

#(2,6)#
#(3,8)#
#(4,5)#
#(2,6)#
Cross-multiply,
#=frac(abs((2*8+3*5+4*6)-(6*3+8*4+5*2)))(2)=frac(5)(2)#

To find the semi-perimeter, we use the distance formula three times (on each side).

#d=sqrt((x_1-x_0)^2+(y_1-y_0)^2)#

So the semiperimeter is:

#frac(sqrt(5)+sqrt(5)+sqrt(10))(2)=frac(2sqrt(5)+sqrt(10))(2)#

Thus, #frac(5)(2)=r(frac(2sqrt(5)+sqrt(10))(2))#

Multiply both sides by #frac(2sqrt(5))(5)#,

#sqrt(5)=(2+sqrt(2))r#

By rationalizing (multiply both sides by #2-sqrt(2)#),

We get that #frac(2sqrt(5)-sqrt(10))(2)=r#

Solution 2:
We recognize that these points form an isoceles right triangle.

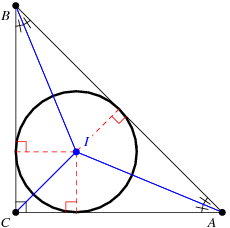
enter image source here

Let's name the point where the perpendicular from #I# to #AC# point #D#.

We first note that:
#BC=AC=sqrt(5)#

The angle bisector through C (which goes through the center of the circle) is also the median of the hypotenuse. An by the Two-Tangent theorem, #AD# is then also half of the hypotenuse, or #frac(sqrt(10))(2)#.

Designating the radius as #r#,

#AC=CD+DA=r+frac(sqrt(10))(2)#

but #AC=sqrt(5)#

So,

#r=sqrt(5)-frac(sqrt(10))(2)=frac(2sqrt(5)-sqrt(10))(2)#

Related questions
See all questions in Area of Inscribed Triangle
Impact of this question
1352 views around the world
You can reuse this answer
Creative Commons License