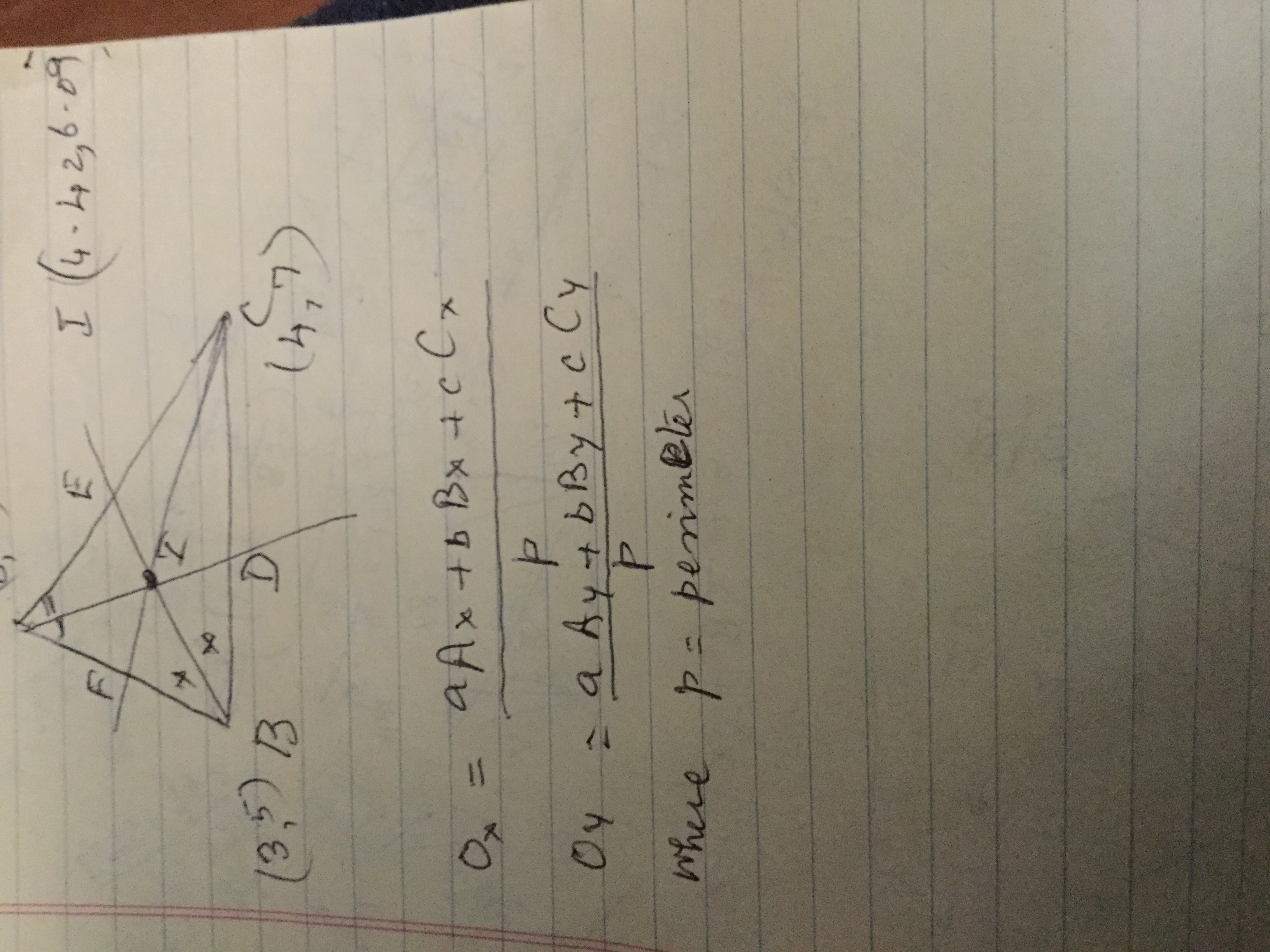A triangle has corners at #(3 , 5 )#, #(4 ,7 )#, and #(8 ,6 )#. What is the radius of the triangle's inscribed circle?
1 Answer
Oct 9, 2017
Coordinates of incenter are (4.42, 6.09)
Explanation:
Let BC = a, AB = c, CA = b & Perimeter = p;
Let the incenter point be O.