A triangle has corners at #(4 , 1 )#, ( 2, 4 )#, and #( 0, 2 )#. What are the endpoints of the triangle's perpendicular bisectors?

1 Answer
Dean R.
Apr 18, 2018

The easy endpoints are the midpoints, #(1,3), (2, 3/2), (3, 5/2)# and the more difficult ones are where the bisectors meet the other sides, including #(8/3,4/3).#

Explanation:

By the perpendicular bisectors of a triangle we presumably mean the perpendicular bisector of each side of a triangle. So there are three perpendicular bisectors for every triangle.

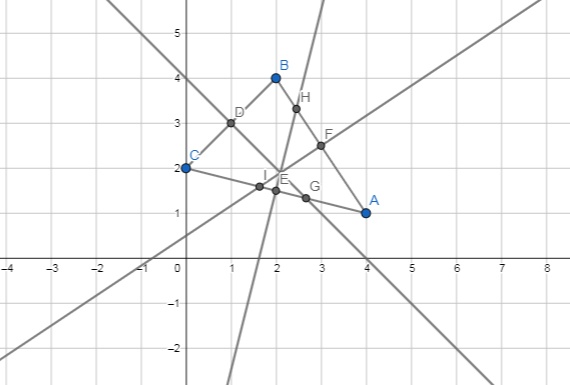
enter image source here

Each perpendicular bisector is defined to intersect one side at its midpoint. It will also intersect one of the other sides. We'll presume those two meets are the endpoints.

The midpoints are

#D=\frac 1 2 ( B+C) = ( (2+0)/2, (4+2)/2) = (1,3)#

# E = \frac 1 2 (A+C) = (2, 3/2) #

# F = \frac 1 2 (A + B) = (3, 5/2) #

This is probably a good place to learn about parametric representations for lines and line segments. #t# is a parameter that can range over the reals (for a line) or from #0# to #1# for a line segment.

Let's label the points #A(4,1)#, #B(2,4)# and #C(0,2)#. The three sides are:

# AB: (x,y) =(1-t)A + tB #

#AB: (x,y)= (1-t)(4,1) + t(2,4) = (4-2t, 1+3t) #

# BC: (x,y) = (1-t)(2,4) + t(0,2) = (2-2t,4-2t)#

# AC: (x,y)=(1-t)(4,1)+t(0,2)=(4-4t, 1+t)#

As #t# goes from zero to one we trace out each side.

Let's work one out. #D# is the midpoint of #BC#,

#D=\frac 1 2 ( B+C) = ( (2+0)/2, (4+2)/2) = (1,3)#

The direction vector from C to B is #B-C=(2,2)#. For the perpendicular, we flip the two coefficients (no effect here because they're both #2#) and negate one. So the parametric equation for the perpendicular

#(x,y) = (1,3) + t(2,-2) = (2u+1,-2u+3)#

(Different line, different parameter.) We can see where this meets each of the sides.

#BC: (2-2t,4-2t)=(2u+1,-2u+3)#

# 1 = 2t+2u#

# 1 = 2t - 2u#

# 2 = 4t #

# t= 1/2#

# t= 1/2# verifies that the perpendicular bisector meets BC at its midpoint.

#AB: (4-2t, 1+3t)= (2u+1,-2u+3)#

#4-2t = 2u+1#

# 2t + 2u = 3 #

# 1+3t = - 2u+3 #

# 3t + 2u = 2 #

Subtracting,

# t = 2-3 = - 1 #

That's outside the range so the perpendicular bisector of BC doesn't hit the side AB.

# AC: 4-4t=2u + 1 quad quad 3 =4t+2u #

# 1+t = -2u + 3 quad quad 2 = t + 2u #

Subtracting,

# 1=3t #

# t = 1/3 #

That gives the other endpoint as

# (4-4t, 1+t) = (8/3, 4/3) #

This is getting long, so I'll leave the other two endpoints to you.

Related questions
See all questions in Perpendicular Bisectors
Impact of this question
2903 views around the world
You can reuse this answer
Creative Commons License