A triangle has corners at #(5 ,1 )#, #(7 ,9 )#, and #(4 ,2 )#. What is the area of the triangle's circumscribed circle?
2 Answers
Area of circumscribed circle of the triangle is
Explanation:
Side
Side
Side
Area of Triangle is
Radius of circumscribed circle is
Area of circumscribed circle is
sq.unit [Ans]
Explanation:
The idea is to find the centre of the circle, then use
We will make use of the circle theorem:
The perpendicular from the radius to a chord bisects the chord
This means that we can find the centre from where the perpendicular bisectors of two of the lines intersect. From here, we can find the square of the radius, and the area.
I'll give the points some names.
Let
First, let's sketch the information we're given.
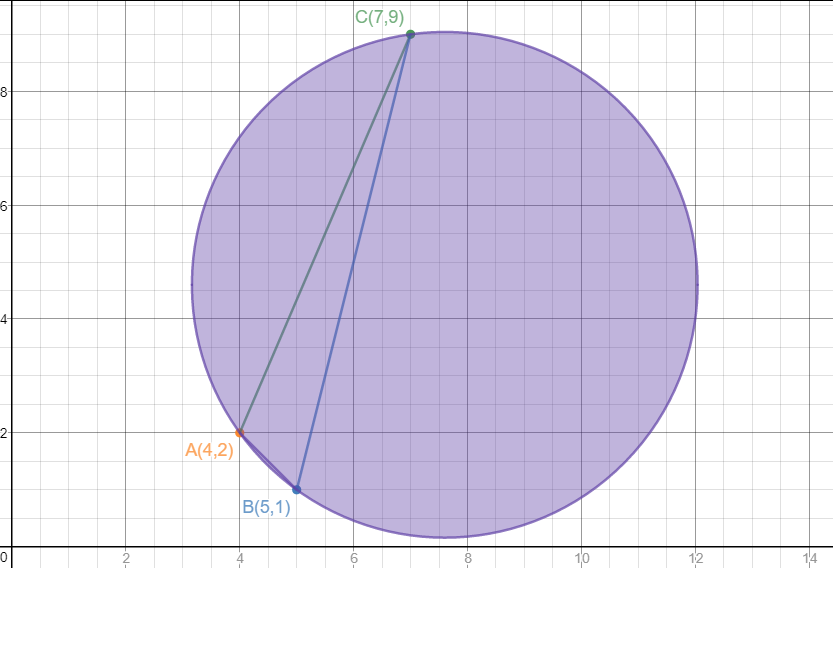
We will begin by finding the equation of the perpendicular bisector of AB.
Now, we will do the same for BC.
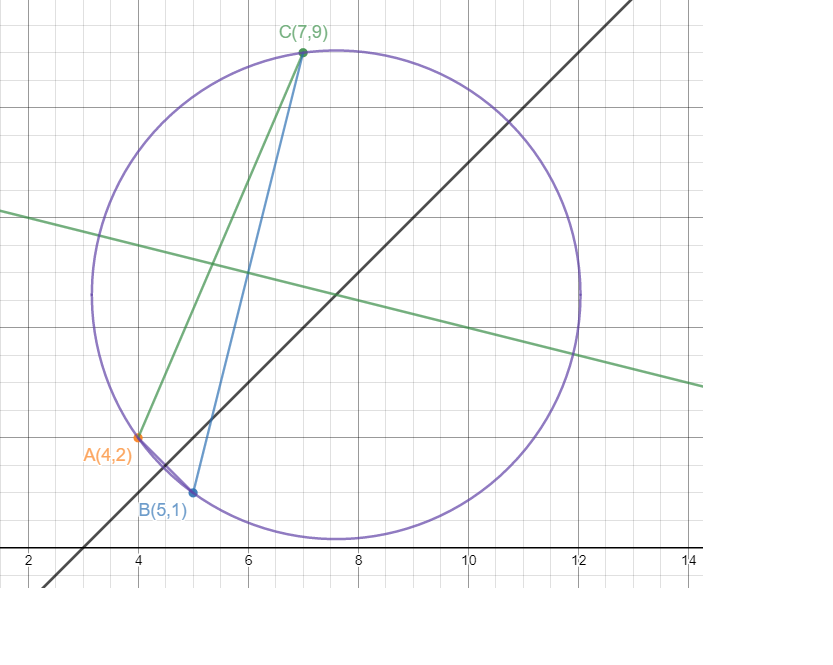
The centre of the circle will be the point at which these two lines intersect, so we solve these equations simultaneously.
So the centre of the centre is
From this, we can work out the radius. In fact, it's easier to work out
becomes
We'll take the centre as
Since
