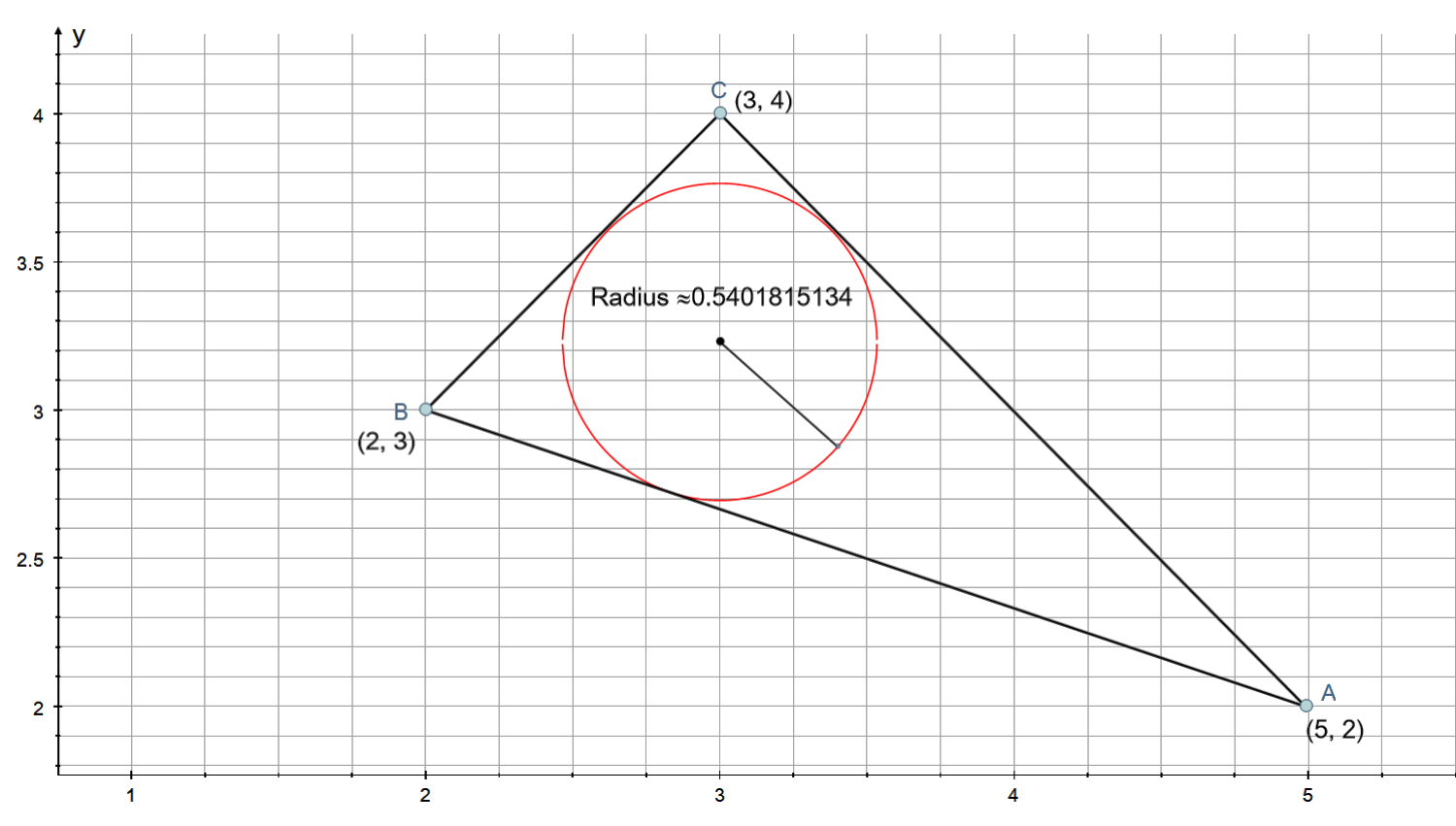
A triangle has corners at #(5 , 2 )#, #(2 ,3 )#, and #(3 ,4 )#. What is the radius of the triangle's inscribed circle?

1 Answer
Somebody N.
Jun 7, 2018

#color(blue)("Radius" ~~0.5401815134)#

Explanation:

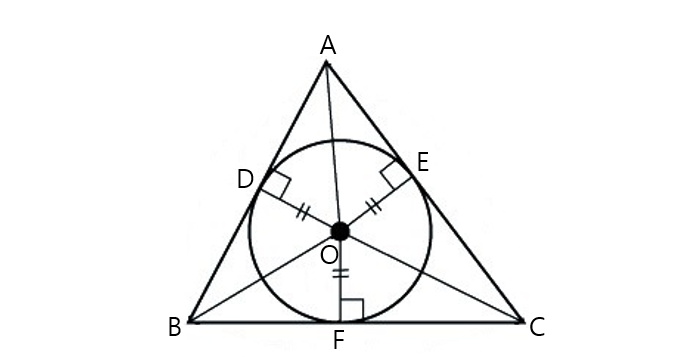
enter image source here

From diagram:

#OD=OE=OF="radius of circle"#

#Delta AOB, Delta AOC, Delta BOC# all have bases that are the sides of #Delta ABC#.

They also all have heights #r# ( the radius of the circle.)

So it follows:

#"Area of " DeltaABC= "Area of "Delta AOB+ Delta AOC+ Delta BOC#

#"Area of " DeltaABC= "1/2AB*r+ 1/2AC*r+ 1/2BC*r#

#"Area of " DeltaABC= "1/2*r(AB+ AC+ BC)#

#"Area of " DeltaABC= "1/2*rxx#perimeter of ABC

Let:

#A=(5,2)# , #B=(2,3)#, #C=(3,4)#

Using the distance formula:

#|AB|=sqrt((2-5)^2+(3-2)^2)=sqrt(10)#

#|BC|=sqrt((3-2)^2+(4-3)^2)=sqrt(2)#

#|AC|=sqrt((3-5)^2+(4-2)^2)=sqrt(8)=2sqrt(2)#

Now we need to find area of #Delta ABC#.

There are different ways we can do this. Having the lengths of the sides we could use Heron's formula, or we could find the height of ABC using line equations. Since we have surds for the lengths of the sides, Heron's formula will be pretty messy and a calculator or computer will be really helpful.

Heron's formula is given as:

#"Area"=sqrt(s(s-a)(s-b)(s-c))#

Where #a,b,c# are the sides of ABC and s is the semi-perimeter.

#s=(a+b+c)/2#

I won't include the calculation for this, I will just give the result.

#"Area"=2#

So to find radius:

#2=1/2xxrxx(sqrt(10)+2sqrt(2)+sqrt(2))#

#r=4/(sqrt(10)+2sqrt(2)+sqrt(2))=(2sqrt(2))/(sqrt(5)+3)~~0.5401815134#

PLOT:

enter image source here

Related questions
See all questions in Area of Inscribed Triangle
Impact of this question
1471 views around the world
You can reuse this answer
Creative Commons License