These are so hard -- who keeps posting them? Let's go with a figure this time. #A(5,3),B(7,8),C(2,1)#
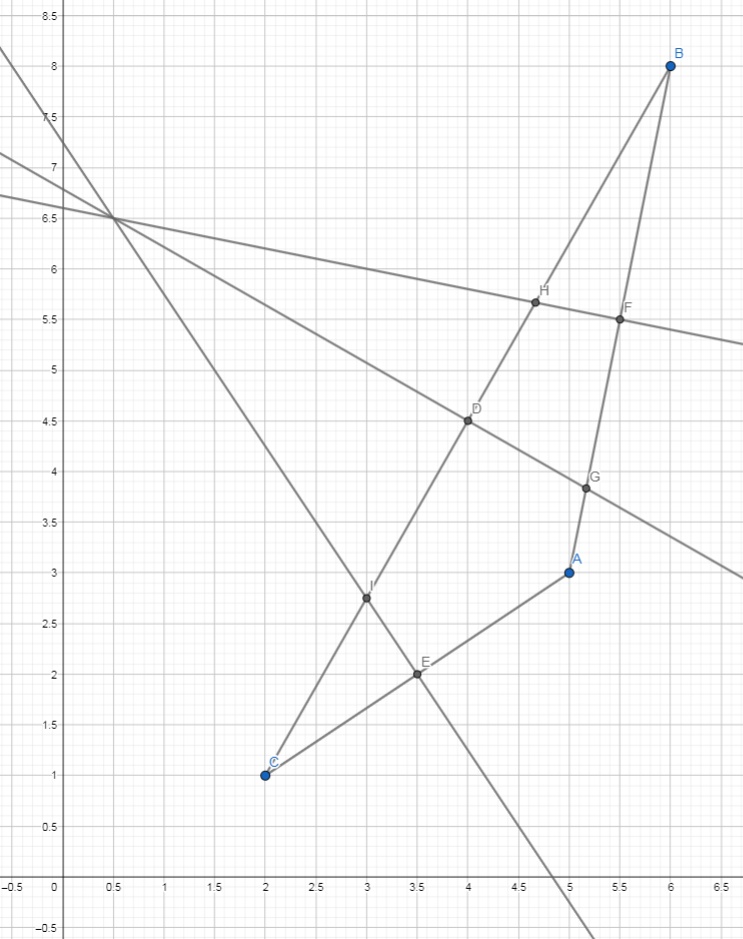
First, the easy endpoints are the midpoints of the sides:
#D=(B+C)/2=(9/2,9/2)#
#E=(A+C)/2=(7/2,2)#
#F=(A+B)/2=(6,11/2)#
Let's write the equations for the sides:
# BC: (y-1)(7-2)=(x-2)(8-1) quad quad -7 x + 5 y = -9 #
# AC: (y-1)(5-2)=(x-2)(3-1) quad quad -2 x + 3 y = - 1 #
#AB: (y-3)(7-5)=(x-5)(8-3) quad quad -5 x + 2 y = - 19 #
For perpendicular bisectors we swap the coefficients on #x# and #y# and negate one. We get the constant by plugging in the midpoint.
# DG bot BC: 5 x + 7y = 5(9/2) + 7(9/2)=54#
# EI bot AC: 3x + 2y = 3(7/2) + 2(2)=29/2#
# FH bot AB: 2 x + 5y = 2(6) + 5(11/2) = 79/2 #
#G# is the meet of #DG# and #AB#:
#5 x + 7y=54#
#-5 x + 2 y = - 19#
#9y = 35#
#y = 35/9#
#x = 1/5 (54 - 7(35/9)) = 241/45 #
#G = (241/45, 35/9) #
# DG=sqrt{(9/2 - 241/45)^2 + (9/2 - 35/9)^2} = {11 sqrt(74)}/90#
Phew. That's one, though it may not be right.
#I# is the meet of #EI# with #BC#
#3x + 2y =29/2 #
# -7 x + 5 y = -9 #
# 30 x + 20 y =145 #
# -28 x + 20 y = -36 #
# 58 x = 181 #
# x= 181/58 #
#y=149/58#
# I=(181/58, 149/58)#
# EI=sqrt{(7/2 - 181/58)^2 + (2 - 149/58)^2} = { 11 sqrt(13)}/58 #
#FH# meets #BC# at #H#
#2 x + 5y = 79/2#
# -7 x + 5 y = -9 #
# 9 x = 97/2 #
# x = 97/18 #
#y = 517/90#
#H=(97/18, 517/90)#
#FH=sqrt((6 - 97/18)^2 + (11/2- 517/90)^2 ) = 11 sqrt{29}/90#


