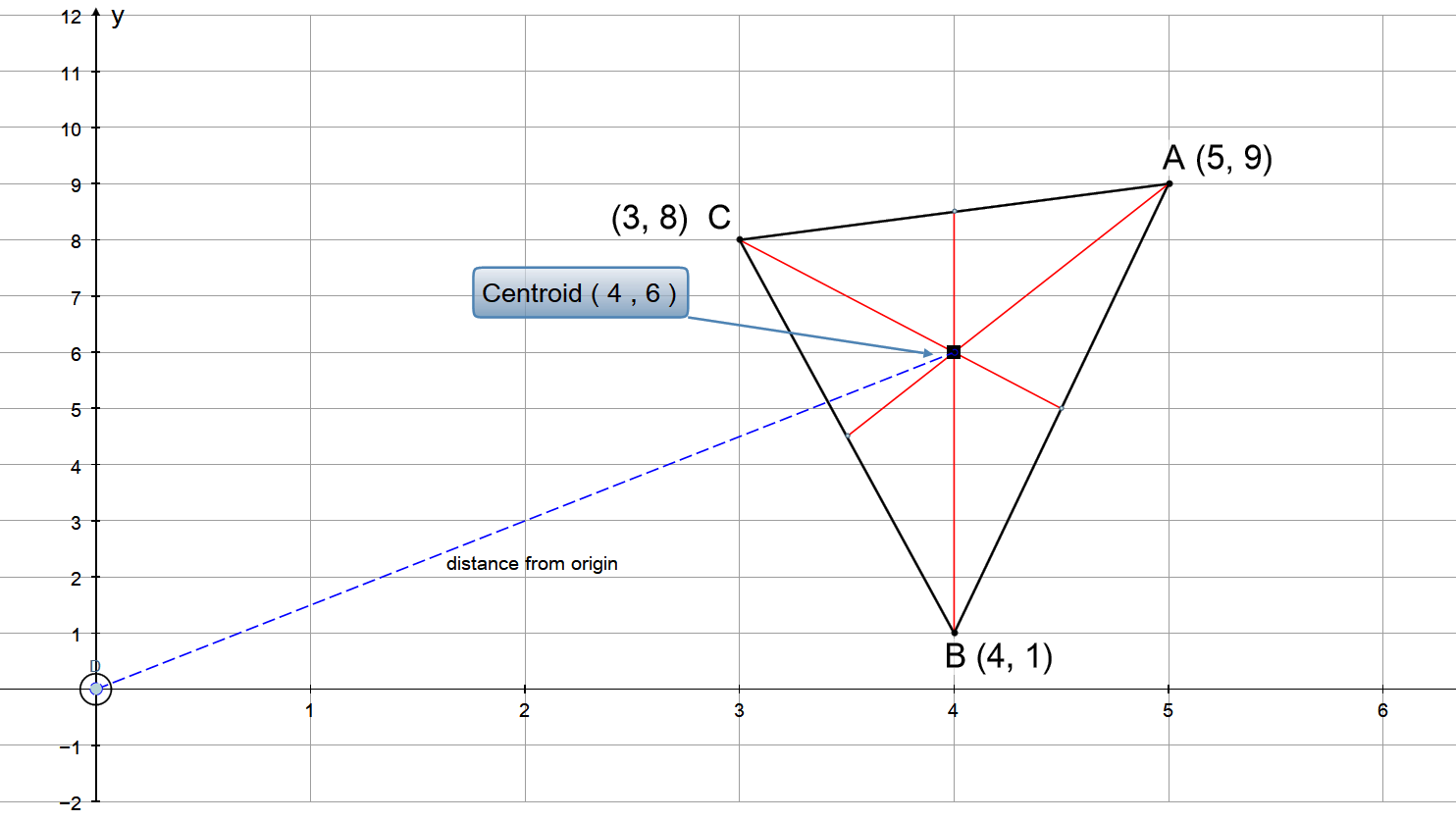
A triangle has corners at #(5 ,9 )#, #(4 ,1 )#, and #(3 ,8 )#. How far is the triangle's centroid from the origin?

1 Answer
Somebody N.
Apr 23, 2018

#color(blue)(2sqrt(13))# units

Explanation:

The centroid is the point where the triangles medians meet. A median is a line through a vertex to the midpoint of the opposite side. A triangle has three medians , but will will only need to find two of these to find the point of intersection, which is the centroid.

Chose two sides:

#AB# and #AC#

Let #A=(5,9) ,B=(4,1), C=(3,8)#

Find the coordinates of the midpoints of these two sides:

The coordinates of the midpoint of a line are given by:

#((x_1+x_2)/2,(y_1+y_2)/2)#

For #AB#

#((5+4)/2,(9+1)/2)=(9/2,5)#

For #AC#

#((5+3)/2,(9+8)/2)=(4,17/2)#

#AB# passes through vertex #C=(3,8)#

#AC# passes through vertex #B=(4,1)#

We now find the equations of two lines using midpoints and vertices.

For #AB#

Gradient:

#(8-5)/(3-9/2)=3/(-3/2)=-2#

Using point slope form of a line:

#(y_2-y_1)=m(x_2-x_1)#

#y-8=-2(x-3)#

#y=-2x+14 \ \ \ \ \ \ \ [1]#

For #AC#

Gradient:

#(1-17/2)/(4-4)=(-15/2)/0#( this is undefined and shows we have a vertical line.

#x=4 \ \ \ \ \ [2]#

Solving simultaneously:

#y=-2(4)+14=>y=6#

Coordinates of centroid:

#(4,6)#

To find the distance from the origin we use the distance formula:

#d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)#

#d=sqrt((0-4)^2+(0-6)^2)=sqrt(52)=2sqrt(13)#

PLOT:

enter image source here

Related questions
See all questions in Distance between Points
Impact of this question
1269 views around the world
You can reuse this answer
Creative Commons License